Топологические преобразования

Топологические преобразования - это операции, применяемые к топологическим пространствам и сохраняющие их ключевые свойства, такие как связность и непрерывность.

Подобные преобразования занимают центральное место в топологии, разделе математики, изучающем свойства пространств, остающиеся неизменными при непрерывных деформациях.

Основные характеристики топологических преобразований:

• Непрерывность
  Топологическое преобразование должно быть непрерывным, то есть малые изменения входных данных вызывают малые изменения результата.
• Сохранение связности и близости
  Такие преобразования сохраняют понятия близости и связности. Если две точки были связаны или находились рядом в исходном пространстве, они останутся в тех же отношениях и после преобразования.
• Деформация без разрывов и склеивания
  Объекты можно растягивать, сжимать или изгибать, но нельзя разрывать или склеивать. Например, с топологической точки зрения пончик можно непрерывно преобразовать в кофейную чашку, так как у обоих объектов есть одно «отверстие».

Применение: Топологические преобразования используются в различных областях, от чистой математики, таких как теория узлов и алгебраическая топология, до изучения свойств объектов, сохраняющихся при непрерывных деформациях.

Типы топологических преобразований

В топологии преобразования классифицируются по тому, какие именно свойства пространства они сохраняют.

Основные типы топологических преобразований включают:

• Гомеоморфизмы
  Гомеоморфизм - это непрерывное преобразование с непрерывным обратным. Оно позволяет взаимно однозначно преобразовывать одно пространство в другое без разрывов или склеивания. Гомеоморфизмы составляют основу топологии. Классический пример - преобразование чашки в пончик.
• Изотопии
  Изотопия - частный случай гомеоморфизма, при котором каждое промежуточное состояние преобразования также является гомеоморфизмом. Например, если плавно перемещать узел вдоль нити, не затягивая и не ослабляя его, каждое положение соответствует изотопии.
• Гомотопии
  Гомотопия описывает непрерывное преобразование одной функции в другую при сохранении основных топологических свойств. Это более общее понятие, чем гомеоморфизм. Пример: растягивание и последующее сжатие пружины, все промежуточные состояния считаются гомотопными.
• Диффеоморфизмы
  Диффеоморфизм - это гомеоморфизм, который является дифференцируемым и имеет дифференцируемое обратное. Он особенно важен в дифференциальной топологии, где исследуется гладкость и дифференцируемость поверхностей. Например, плавное преобразование сферы в вытянутый эллипсоид.

Каждый тип преобразований отражает разные аспекты непрерывности и деформируемости пространств и функций. Их использование зависит от контекста: общей, алгебраической или дифференциальной топологии.

Различия между геометрическими и топологическими преобразованиями

Геометрические и топологические преобразования различаются как по своим свойствам, так и по областям применения.

• Геометрические преобразования
  Геометрические преобразования изменяют положение или форму объектов, сохраняя при этом геометрические характеристики, такие как расстояния, углы и пропорции. К ним относятся параллельные переносы, повороты, отражения и масштабирование.

  Например, вращение сохраняет расстояния и углы, но изменяет ориентацию фигуры.

• Топологические преобразования
  Топологические преобразования меняют форму пространства, сохраняя его топологические свойства, такие как связность и непрерывность, но не обязательно расстояния или углы. Эти преобразования значительно гибче, так как допускают растяжения и деформации без разрывов и склеивания.

  Так, в топологии пончик и чашка считаются эквивалентными, поскольку оба имеют одно отверстие.

Если геометрические преобразования сосредоточены на сохранении конкретных метрических величин, то топологические изучают деформации, сохраняющие общую структуру и непрерывность независимо от формы или размеров.

Могут ли преобразования быть одновременно геометрическими и топологическими?

Да, некоторые преобразования одновременно сохраняют геометрические характеристики, такие как углы, длины и формы, и являются непрерывными, сохраняя топологические свойства, например связность и непрерывность.

Примеры таких преобразований:

• Изометрии
  Изометрии, включая параллельные переносы, вращения и отражения, сохраняют расстояния между точками и углы, поэтому они одновременно геометрические и топологические. Они представляют собой гомеоморфизмы, так как имеют непрерывные обратные преобразования.
  
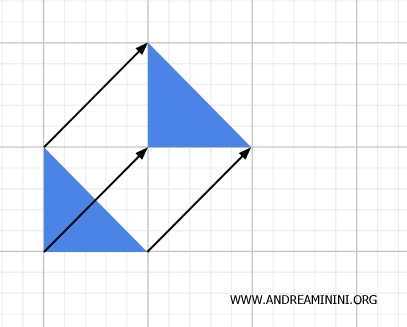
• Сходственные преобразования
  Сходственные преобразования изменяют размер объекта, но сохраняют его форму, углы и пропорции. Они считаются геометрическими, однако с топологической точки зрения также являются непрерывными и сохраняют связность.

Эти примеры показывают, что геометрические и топологические свойства не всегда строго разделены. В некоторых случаях одно и то же преобразование может быть как геометрически значимым, так и топологически корректным.

И так далее.