Дискретная топология
Дискретная топология T - это топология, в которой любое подмножество множества X считается открытым. Иными словами, она включает все возможные подмножества X и поэтому является самой «богатой» из всех возможных топологий.
В дискретной топологии каждое подмножество множества X - открытое. Это значит, что каждая точка пространства изолирована, и между элементами нет понятия «близости» или непрерывности. Любое расположение точек допустимо.
Примечание. Чтобы система множеств считалась топологией, она должна удовлетворять трём условиям:
- Пустое множество и всё множество X входят в топологию T.
- Объединение любого числа множеств из T тоже принадлежит T.
- Пересечение любого конечного числа множеств из T также принадлежит T.
Топология называется дискретной, потому что она рассматривает элементы множества X как полностью независимые друг от друга. Здесь нет постепенного перехода от одной точки к другой - каждая из них существует сама по себе.
Дискретная топология - это самая полная форма топологии, так как не существует другой, которая содержала бы больше открытых множеств.
Примечание. Эти условия задают основу для описания открытых множеств и позволяют формально говорить о непрерывности и связности в пространстве.
Главное свойство дискретной топологии
В дискретной топологии любое подмножество топологического пространства является одновременно открытым и замкнутым.
Это происходит потому, что если все подмножества считаются открытыми, то и их дополнения (в пределах множества X) тоже открыты. А множество называется замкнутым, если его дополнение открыто.
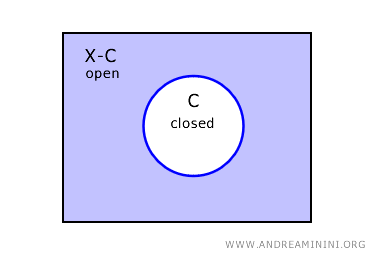
Отсюда следует: если дополнение любого множества открыто, то и само множество замкнуто. Таким образом, каждое множество в дискретной топологии является «клопеном» - то есть одновременно открытым и замкнутым.
Примечание. В дискретной топологии это свойство распространяется на все подмножества без исключений. Каждая точка считается открытой, любое их объединение - тоже открытое. Поскольку дополнение любого подмножества является подмножеством X и, следовательно, открытым, то каждое множество оказывается и замкнутым.
Пример
Рассмотрим пример дискретной топологии на небольшом множестве X, состоящем из трёх элементов:
$$ X = \{a, b, c\} $$
Множество всех подмножеств X (так называемый булеан) включает:
- пустое множество: \(\emptyset\)
- одноэлементные множества: \(\{a\}\), \(\{b\}\), \(\{c\}\)
- двухэлементные множества: \(\{a, b\}\), \(\{a, c\}\), \(\{b, c\}\)
- всё множество: \(\{a, b, c\}\)
В дискретной топологии каждое из этих подмножеств считается открытым. Следовательно:
$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\} $$
Эта структура действительно является топологией: она включает пустое множество и всё множество X, а объединения и конечные пересечения её элементов остаются внутри T. Так как все подмножества открыты, ограничений на «близость» или непрерывность между элементами здесь нет.
Возьмём, например, подмножество $ \{ a \} $. По определению оно открыто. Его дополнение $ X / \{a\} = \{b, c\} $ также открыто, следовательно, $ \{ a \} $ замкнуто. Мы видим, что в дискретной топологии множество $ \{ a \} $ одновременно открыто и замкнуто.
Аналогично, это верно для любого другого подмножества множества X.