Гомеоморфизмы в топологии

Гомеоморфизм это отображение в топологии, представляющее собой биективную непрерывную функцию, обратная к которой также непрерывна.

Иными словами, одно топологическое пространство можно преобразовать в другое и вернуть в исходное состояние без «разрывов» и «склеиваний».

Проще говоря, гомеоморфизм позволяет плавно преобразовать одно пространство в другое, не нарушая его целостности.

Например, чашка с ручкой и пончик (тор) считаются гомеоморфными объектами. Одну фигуру можно непрерывно деформировать в другую, не разрушая и не приклеивая части.

С точки зрения топологии, эти формы эквивалентны, поскольку каждая из них содержит одно отверстие: у пончика это центральное отверстие, у чашки пространство в ручке. Если «размять» чашку вдоль ручки, из неё можно получить пончик.

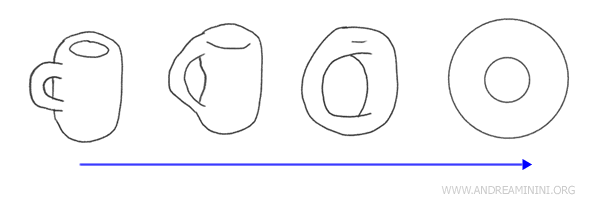
Если два топологических пространства связаны гомеоморфизмом, их называют гомеоморфными. Это означает, что с точки зрения топологии они идентичны, даже если геометрически выглядят по-разному.

Основные свойства гомеоморфизма

Гомеоморфизм обладает следующими ключевыми свойствами:

• Биективность
  Между элементами двух пространств устанавливается взаимно однозначное соответствие: каждому элементу одного пространства соответствует ровно один элемент другого и наоборот.
• Непрерывность
  Гомеоморфизм является непрерывным отображением, то есть небольшие изменения входных данных приводят к небольшим изменениям результата.
• Непрерывность обратного отображения
  Обратная функция к гомеоморфизму также должна быть непрерывной, чтобы преобразование можно было выполнять в обе стороны без потери непрерывности.
• Сохранение топологических свойств
  Гомеоморфизм сохраняет такие фундаментальные свойства, как связность, компактность и непрерывность. Внутренняя структура исходного пространства остаётся неизменной в преобразованном.

Таким образом, гомеоморфизм это непрерывное и обратимое отображение между двумя топологическими пространствами \(X\) и \(Y\), при котором обратное также непрерывно. Это гарантирует сохранение топологических свойств обоих пространств.

Иными словами, гомеоморфизм это способ «переформировать» одно пространство в другое, не разрушая его структуры. Это своего рода «идеальное соответствие» между двумя фигурами.

Напомним определение непрерывности в топологии:

Пусть заданы два топологических пространства \(X\) и \(Y\). Функция \(f: X \to Y\) называется непрерывной, если для любого открытого множества \(V\) в \(Y\) прообраз \(f^{-1}(V)\) является открытым множеством в \(X\).

Иными словами, непрерывное отображение в топологии сохраняет структуру открытых множеств при переходе из одного пространства в другое.

Таким образом, понятие непрерывности в топологии является более общим и абстрактным, чем в математическом анализе.

Примечание: В анализе непрерывность определяется через расстояние между точками. В топологии же она основана на понятии открытых множеств и не требует метрики.

Наглядный пример

Рассмотрим простой пример, иллюстрирующий понятие гомеоморфизма и непрерывности с помощью открытых множеств.

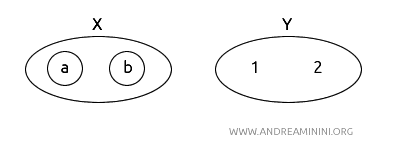
Пусть \(X = \{a, b, c, d\}\) и \(Y = \{1, 2\}\) два топологических пространства.

• В пространстве \(X\) открыты множества: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• В пространстве \(Y\) открыты множества: \(\{\}, \{1\}, \{1, 2\}\).

Функция \(f: X \rightarrow Y\) будет непрерывной, если прообраз каждого открытого множества в \(Y\) открыт в \(X\).

Определим \(f: X \rightarrow Y\) так:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Для наглядности изобразим функцию \(f\) и открытые множества на схемах.

 

Пример

Рассмотрим следующие два топологических пространства:

• \( X = (a, b) \) с топологией \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) с топологией \( T_Y = \{\emptyset, Y\} \).

Определим функцию \( f: X \to Y \) так, что \( f(a) = 1 \), а \( f(b) = 2 \).

Функция \( f \) очевидно биективна, так как каждому элементу множества \( X \) соответствует единственный элемент множества \( Y \) и наоборот.

Примечание: На рисунке открытые множества обозначены окружностями. Например, в \( X \) открыты множества {a, b}, {a} и {b}, а в \( Y \) открытым является только множество {1, 2}. По определению, пустое множество всегда открыто, но на схеме оно опущено для упрощения.

Теперь проверим, является ли функция \( f \) и её обратная \( f^{-1} \) непрерывными.

• Непрерывность функции \( f \)
  Чтобы установить непрерывность \( f \), нужно убедиться, что прообраз каждого открытого множества из \( Y \) является открытым в \( X \). В \( Y \) открыты множества \( \emptyset \) и \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), это открытое множество в \( T_X \).
  • \( f^{-1}(Y) = X \), также открытое множество в \( T_X \).
  Поскольку прообразы всех открытых множеств в \( Y \) открыты в \( X \), функция \( f \) является непрерывной.
• Непрерывность обратной функции \( f^{-1} \)
  Рассмотрим обратное отображение \( f^{-1}: Y \to X \), где \( f^{-1}(1) = a \), \( f^{-1}(2) = b \).
  Проверим, сохраняет ли оно непрерывность, то есть открыты ли прообразы всех открытых множеств из \( X \) в \( Y \). В \( X \) открыты множества \( \emptyset \), \(\{a\}\), \(\{b\}\) и \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), открытое множество в \( T_Y \).
  • \( f^{-1}(\{a\}) = \{1\} \), которое не является открытым в \( T_Y \), поскольку единственное открытое множество, содержащее 1, это всё \( Y \).
  • \( f^{-1}(\{b\}) = \{2\} \), также не открытое в \( T_Y \) по той же причине.
  • \( f^{-1}(X) = Y \), открытое множество в \( T_Y \).
  Следовательно, прообразы \(\{a\}\) и \(\{b\}\) не являются открытыми в \( Y \), и функция \( f^{-1} \) не непрерывна.

Таким образом, функция \( f \) биективна и непрерывна, но её обратное отображение \( f^{-1} \) непрерывным не является. Следовательно, \( f \) не является гомеоморфизмом.

Этот пример показывает, что биективность и непрерывность функции не гарантируют непрерывность обратного отображения.

Примечание: В данном случае отсутствие непрерывности у \( f^{-1} \) связано с разницей в структуре топологий: в \( X \) определены более «тонкие» открытые множества (\(\{a\}\) и \(\{b\}\)), тогда как топология \( Y \) грубее и включает только \( \emptyset \) и \( Y \).

Пример 2

Рассмотрим другую пару топологических пространств:

• \( X = (a, b) \) с топологией \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) с топологией \( T_Y = \{\emptyset, \{1\}, Y\} \).

Определим функцию \( f: X \to Y \) как \( f(a) = 1 \) и \( f(b) = 2 \).

Функция \( f \) снова биективна, так как каждому элементу множества \( X \) соответствует один элемент множества \( Y \) и наоборот.

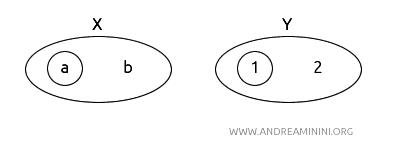
Проверим непрерывность \( f \) и её обратной функции \( f^{-1} \).

• Непрерывность функции \( f \)
  Необходимо проверить, что прообразы всех открытых множеств из \( Y \) открыты в \( X \). В \( Y \) открыты множества \( \emptyset \), \(\{1\}\) и \( Y \):
  • \( f^{-1}(\emptyset) = \emptyset \), открыто в \( T_X \).
  • \( f^{-1}(Y) = X \), открыто в \( T_X \).
  • \( f^{-1}(\{1\}) = \{a\} \), открыто в \( T_X \).
  Таким образом, функция \( f \) непрерывна.
• Непрерывность обратной функции \( f^{-1} \)
  Рассмотрим обратное отображение \( f^{-1}: Y \to X \), где \( f^{-1}(1) = a \), \( f^{-1}(2) = b \). Проверим, открыты ли прообразы открытых множеств из \( X \) в \( Y \). В \( X \) открыты множества \( \emptyset \), \(\{a\}\) и \( X \):
  • \( f^{-1}(\emptyset) = \emptyset \), открыто в \( T_Y \).
  • \( f^{-1}(\{a\}) = \{1\} \), открыто в \( T_Y \).
  • \( f^{-1}(X) = Y \), открыто в \( T_Y \).
  Следовательно, функция \( f^{-1} \) непрерывна.

В этом случае \( f \) биективна, непрерывна, а её обратное отображение \( f^{-1} \) также непрерывно. Поэтому \( f \) является гомеоморфизмом.

Отличие от предыдущего примера заключается в выборе топологий для пространств \( X \) и \( Y \).

Примечание: Этот пример демонстрирует, что при корректном выборе топологий для \( X \) и \( Y \) можно получить биективное и непрерывное отображение с непрерывным обратным, в отличие от первого случая, где это условие не выполнялось.

Отличие гомеоморфизмов от других топологических преобразований

Хотя термин «гомеоморфизм» иногда употребляется в широком смысле как синоним топологических преобразований, на самом деле это частный, более строгий их вид.

Гомеоморфизмы и топологические преобразования близки по сути, но не совпадают:

• Топологические преобразования
  Это более широкий класс отображений, которые могут изменять форму пространства, сохраняя при этом его основные топологические свойства, такие как связность и непрерывность. К ним относятся не только гомеоморфизмы, но и изотопии, гомотопии и диффеоморфизмы.
• Гомеоморфизмы
  Гомеоморфизм представляет собой биективное и непрерывное отображение с непрерывной обратной функцией. Он позволяет взаимно преобразовывать пространства без разрывов и склеиваний. С топологической точки зрения такие пространства эквивалентны, даже если их геометрическая форма различается.

Каждый гомеоморфизм является топологическим преобразованием, но не каждое топологическое преобразование является гомеоморфизмом.

Некоторые топологические преобразования обладают свойствами, которые не соответствуют строгим критериям гомеоморфизма.

Дополнительные замечания

Ниже приведены некоторые важные пояснения, касающиеся гомеоморфизмов:

• Топологические свойства
  Топологическое свойство - это характеристика топологического пространства, сохраняющаяся при гомеоморфизмах. Другими словами, если два пространства гомеоморфны, то есть между ними существует взаимно однозначное непрерывное отображение с непрерывной обратной функцией, они обладают одними и теми же топологическими свойствами.
• Теорема Хаусдорфа о гомеоморфизмах
  Согласно этой теореме, если \( f: X \to Y \) - гомеоморфизм и пространство \( X \) является хаусдорфовым, то и \( Y \) также хаусдорфово. Это связано с тем, что гомеоморфизмы сохраняют все топологические свойства, включая свойство Хаусдорфа.
• Аналогом гомеоморфизма в абстрактной алгебре является изоморфизм групп. В изоморфизме сохраняется алгебраическая структура операций, тогда как гомеоморфизм сохраняет структуру открытых множеств в топологических пространствах.

И так далее.