Топология с прямоугольной базой

Топология с прямоугольной базой на плоскости R² рассматривает открытые множества как объединения открытых прямоугольников. Каждый прямоугольник задаётся произведением двух открытых интервалов по осям координат. Такой подход удобно описывает локальную структуру пространства и помогает интуитивно понять, как устроена плоскость.

Основу этой топологии составляют открытые прямоугольные окрестности. Это самые простые открытые множества, на которых строится вся топологическая структура плоскости.

Идея проста. Множество $ U \subseteq \mathbb{R}^2 $ считается открытым, если для любой точки $ (x, y) $ внутри $ U $ найдётся открытый прямоугольник, который содержит эту точку и полностью лежит в $ U $. Если такое можно сделать для каждой точки, то множество открыто.

Открытые прямоугольники выполняют роль базовых элементов, из которых складывается топология евклидовой плоскости.

$$ B= \{ (a, b) \times (c, d) | a

Здесь $ a, b, c, d $ - действительные числа. Неравенства $ a < b $ и $ c < d $ задают границы прямоугольника и определяют его положение на плоскости.

Такой базис является альтернативой стандартной топологии, где открытые множества задаются через открытые шары. Несмотря на разницу в форме, обе структуры приводят к одной и той же топологии на $ \mathbb{R}^2 $.

Note: Выбор формы базовых множеств не меняет сути. Шары или прямоугольники - обе коллекции создают корректную топологию, если из них можно получить все открытые множества плоскости.

Пример открытого прямоугольника

Открытый прямоугольник - это декартово произведение двух открытых интервалов по осям координат.

Возьмём интервалы $ (1, 3) $ по оси $ x $ и $ (2, 4) $ по оси $ y $.

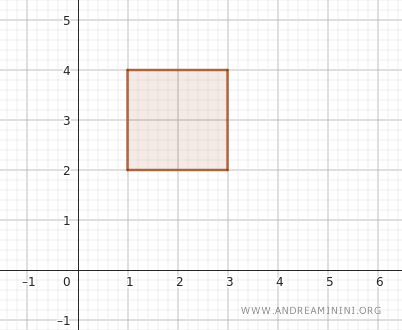
an example of an open rectangle

Такой прямоугольник содержит все точки $ (x, y) $, где $ x $ находится между 1 и 3, а $ y $ - между 2 и 4. Это можно записать как $ (1, 3) \times (2, 4) $.

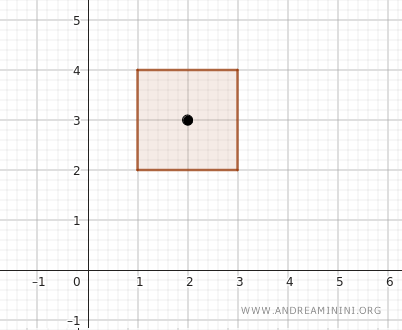
the point (2,3)

Рассмотрим точку $ (2, 3) $. Координата $ x $ лежит между 1 и 3, а $ y $ - между 2 и 4. Следовательно, точка принадлежит этому открытому прямоугольнику.

Note: Граница прямоугольника не входит в него. Поэтому точки вида $ (1, y) $, $ (3, y) $, $ (x, 2) $ и $ (x, 4) $ всегда остаются за пределами открытого прямоугольника.