Топология открытых множеств
Топология T на множестве X это семейство подмножеств X, которые считаются открытыми и удовлетворяют двум основным правилам:
- пустое множество Ø и всё множество X всегда объявляются открытыми;
- объединение и пересечение любого конечного числа открытых множеств тоже должны быть открытыми.
Проще говоря, топология T состоит только из подмножеств X, объявленных открытыми, и не нарушает эти правила. Если семейство подмножеств замкнуто относительно объединения и пересечения, его можно считать топологией.
Семейство множеств это множество, элементы которого сами являются множествами или подмножествами.
В этом случае X вместе с топологией T образуют топологическое пространство. Обычно его записывают как пару (X,T).
Замечание. В неформальной речи часто говорят, что X это топологическое пространство. Но строгое определение включает два объекта: множество X и топологию T как семейство его подмножеств.
Почему пустое множество считается открытым
Пустое множество всегда объявляется открытым по определению. Это соглашение позволяет сохранить логическую целостность и удобство всех последующих построений в топологии.
Наглядный пример
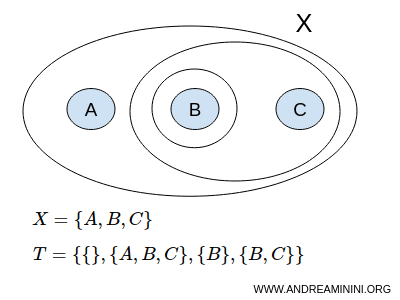
Пусть множество X состоит из трёх элементов A, B и C:
$$ X = \{ A,B,C \} $$
Рассмотрим возможную топологию T. Пусть в неё входят следующие подмножества: { }, {A,B,C}, {B}, {B,C}
$$ T = \{ \{ \}, \{A,B,C\}, \{B\}, \{B,C\} \} $$
Пустое множество Ø и всё множество {A,B,C} здесь присутствуют. Они считаются открытыми по определению. Остальные подмножества также открыты, поскольку мы включили их в топологию T.
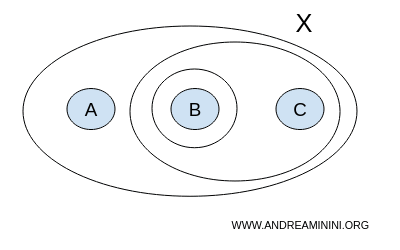
Теперь проверим, замкнута ли T относительно объединения и пересечения. Рассмотрим объединения:
$$ \{ B \} \cup \{ B, C \} = \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} = \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} = \{ B \} \subseteq T $$
Все результаты принадлежат T, значит, семейство замкнуто относительно объединения. Аналогично проверяем пересечение:
$$ \{ B \} \cap \{ B, C \} = \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} = \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} = \{ \} \subseteq T $$
Мы снова получаем множества, входящие в T. Значит, правила соблюдены и T является топологией на X.
Когда семейство не является топологией
Рассмотрим теперь другое семейство тех же подмножеств, но добавим множество {A}:
$$ T = \{ \{ \}, \{A,B,C\}, \{A\}, \{B\}, \{B,C\} \} $$
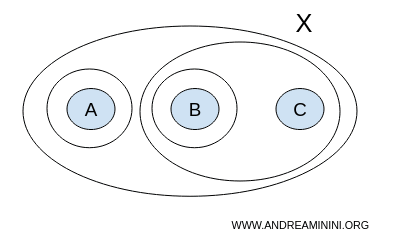
Проверим объединения. Например,
$$ \{ A \} \cup \{ B \} = \{ A,B \} $$
Полученное множество {A,B} не входит в T. Значит, семейство не замкнуто относительно объединения и нарушает одно из ключевых условий.
Поэтому такое семейство T не является топологией множества X.
Тот же метод проверки используется для любых множеств. Если семейство открытых подмножеств проходит обе проверки, оно образует топологию. В противном случае топологии нет.