Замыкание множества

Замыканием множества \( A \) в топологическом пространстве \( X \) называют пересечение всех замкнутых множеств, содержащих \( A \). Это пересечение принято обозначать символом \( \text{Cl}(A) \).

Проще говоря, замыкание множества A это наименьшее по включению замкнутое множество, которое полностью охватывает A.

Любое замкнутое множество, содержащее A, обязательно включает в себя и его замыкание.

Примечание: Это свойство напрямую следует из самого определения замыкания как пересечения всех замкнутых множеств, содержащих A. Таким образом, замыкание можно интерпретировать как максимально «плотную» замкнутую оболочку вокруг множества A.

В формальной записи замыкание множества A задаётся так:

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ и } C \text{ замкнуто в } X \} $$

Здесь \( \text{Cl}(A) \) обозначает замыкание множества \( A \), а символ \( \bigcap \) указывает на пересечение всех замкнутых множеств \( C \), содержащих \( A \).

Замыкание множества \( A \) включает само множество \( A \), а также все его предельные точки в пространстве \( X \).

Примечание: Важно подчеркнуть, что замыкание множества \( A \) определяется прежде всего топологией пространства \( X \), а не внутренними свойствами самого множества. Поэтому при разных топологиях на одном и том же носителе результат может быть различным.

Наглядный пример

Рассмотрим множество \( A = (0, 1) \) в пространстве действительных чисел \( \mathbb{R} \), снабжённом стандартной топологией.

Это открытый интервал, содержащий все действительные числа строго между 0 и 1.

В этом случае замыканием множества \( A \) является отрезок \( [0, 1] \).

$$ \text{Cl}(A) = [0,1] $$

Он состоит из самого интервала \( (0,1) \) и его предельных точек, то есть точек 0 и 1.

Примечание: В стандартной топологии на \( \mathbb{R} \) замкнутыми считаются множества, содержащие все свои предельные точки. Предельная точка множества это такая точка, что любая её окрестность содержит хотя бы одну отличную от неё точку данного множества. Например, пересечение замкнутых отрезков [0,2] и [-1,1] даёт отрезок [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ Меньшего замкнутого отрезка, содержащего (0,1), не существует.

Пример 2

Рассмотрим множество \( A = [0, 1) \) в \( \mathbb{R} \) со стандартной топологией.

Оно содержит все действительные числа от 0 включительно до 1 не включительно. Это полуинтервал, замкнутый слева и открытый справа.

Замыкание этого множества снова совпадает с отрезком $ [0,1] $.

$$ \text{Cl}(A) = [0,1] $$

Причина в том, что точка 0 уже принадлежит A, а точка 1 является его предельной точкой, но в само множество не входит.

Таким образом, замыкание множества A добавляет недостающую граничную точку и даёт наименьшее замкнутое множество, содержащее A.

Примечание: Этот результат хорошо иллюстрирует общее правило замыкания, согласно которому в замыкание входят все предельные точки множества. Например, пересечение отрезков [0,2] и [-1,1] равно [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$

Пример 3

Теперь рассмотрим то же множество \( A = [0,1) \), но в пространстве \( X \) с дискретной топологией.

В дискретной топологии каждое подмножество пространства является одновременно открытым и замкнутым.

• Открытое множество
  Поскольку в дискретной топологии любое подмножество \( X \) открыто, множество A также является открытым.
• Замкнутое множество
  По той же причине любое подмножество \( X \) является замкнутым, так как его дополнение открыто. Следовательно, множество A замкнуто.

Таким образом, в дискретной топологии каждое множество является одновременно открытым и замкнутым, то есть клопеном.

Отсюда следует, что замыкание множества \( A \) совпадает с самим множеством \( A \), поскольку для «дозамыкания» не требуется добавлять новые точки.

$$ \text{Cl}(A) = [0,1) $$

Наименьшее замкнутое множество, содержащее \( A \), в этом случае совпадает с самим \( A \).

Примечание: Этот пример наглядно показывает, насколько сильно выбор топологии влияет на понятие замыкания. Свойство быть замкнутым определяется не самим множеством \( A \), а топологической структурой пространства \( X \).

Пример 4

Рассмотрим топологическое пространство \( X = \{a, b, c \} \), снабжённое дискретной топологией.

В такой топологии каждое подмножество \( X \) является открытым:

• \( \emptyset \) и \( \{a, b, c \} \) открыты по определению.
• Одноточечные множества \( \{a\} \), \( \{b\} \), \( \{c\} \) также являются открытыми.
• Любые их объединения, например \( \{a, b\} \), \( \{a, c\} \), \( \{b, c\} \), тоже открыты.

Кроме того, каждое подмножество \( X \) является и замкнутым, поскольку его дополнение также открыто.

Это означает, что в дискретной топологии любое множество является одновременно открытым и замкнутым.

Рассмотрим множество \( A = \{b, c\} \). Оно открыто и замкнуто по тем же причинам, что и любое другое подмножество пространства \( X \).

Замыкание множества \( A \), определяемое как пересечение всех замкнутых множеств, содержащих \( A \), не требует добавления новых элементов.

Следовательно, замыкание множества \( A \) совпадает с самим множеством:

\[ Cl(A) = \{b, c\} \]

В этой топологии операция замыкания не изменяет множество, так как оно уже является замкнутым.

Примечание: Для проверки заметим, что замкнутыми множествами, содержащими \( A \), являются \( \{b, c\} \) и \( \{a,b,c\} \). $$ Cl(A) = \{b,c\} \cap \{a,b,c\} = \{b, c\} $$ Их пересечение в точности совпадает с \( A \), что подтверждает равенство \( Cl(A) = A \).

Теорема о замыкании множества

В топологическом пространстве \( X \) точка \( y \) принадлежит замыканию подмножества \( S \), обозначаемому \( \text{Cl}(S) \), тогда и только тогда, когда любое открытое множество \( U \), содержащее \( y \), имеет непустое пересечение с \( S \): \( y \in \text{Cl}(S) \iff \forall \ U \text{ открытое, } y \in U \Rightarrow U \cap S \neq \emptyset \).

Говоря интуитивно, точка \( y \) лежит в замыкании множества \( S \) в том и только в том случае, если её невозможно «изолировать» от \( S \) с помощью открытой окрестности.

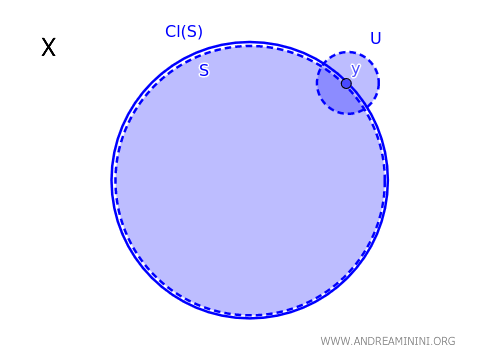
Теорема даёт удобный практический критерий для проверки принадлежности точки замыканию множества в произвольном топологическом пространстве.

Доказательство

• Необходимость: Пусть \( y \in \text{Cl}(S) \). По определению замыкания каждая открытая окрестность точки \( y \) обязана пересекаться с множеством \( S \). Это отражает саму идею замыкания, которое включает не только точки множества, но и все его предельные точки.
• Достаточность: Пусть теперь каждая открытая окрестность точки \( y \) пересекается с \( S \). Тогда \( y \) либо принадлежит самому множеству \( S \), либо является его предельной точкой. В обоих случаях, по определению, \( y \in \text{Cl}(S) \).

Примечание: Теорема о замыкании является одной из базовых в общей топологии. Она связывает понятия замыкания и открытых множеств и широко применяется при изучении непрерывных отображений, сходимости и топологических инвариантов.

Пример

Рассмотрим множество \( A = (0, 2) \) в стандартной топологии на \( \mathbb{R} \). Это обычный открытый интервал на числовой прямой.

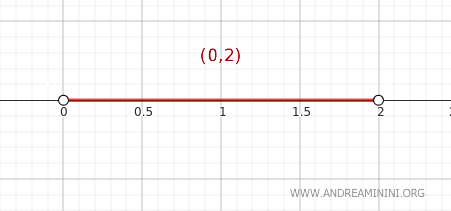
Проверим, принадлежит ли точка \( y \) замыканию множества \( A \).

В качестве конкретного примера возьмём точку \( y = 2 \).

Согласно теореме, \( y \in \text{Cl}(A) \) тогда и только тогда, когда любая открытая окрестность \( U \), содержащая точку \( y \), пересекается с множеством \( A \).

1. Рассмотрение окрестностей точки \( y \): Возьмём любую открытую окрестность точки \( 2 \), например интервалы \( (1.9, 2.1) \), \( (1.95, 2.05) \), \( (1.99, 2.01) \). Все они содержат точки из интервала \( (0, 2) \).
2. Проверка условия теоремы: Поскольку каждая такая окрестность имеет непустое пересечение с \( A \), условие теоремы выполняется.

Следовательно, точка \( y = 2 \) принадлежит замыканию множества \( A \).

$$ y \in \text{Cl}(A) $$

Действительно, замыкание множества \( A \) равно замкнутому отрезку \( \text{Cl}(A) = [0, 2] \), который содержит точку \( 2 \).

Свойства замыкания в топологических пространствах

Ниже перечислены основные свойства операции замыкания, а также важные соотношения между замыканием и внутренностью множества.

• Внутренность дополнения и дополнение замыкания
  Внутренность дополнения множества \( A \) совпадает с дополнением его замыкания: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$
• Замыкание дополнения и дополнение внутренности
  Замыкание дополнения множества \( A \) совпадает с дополнением его внутренности: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$

Ключевые наблюдения

Приведём несколько фундаментальных свойств замыкания, которые часто используются на практике.

• Если C замкнуто в X и A ⊆ C, то Cl(A) ⊆ C
  Если замкнутое множество \( C \) содержит \( A \), то оно обязательно содержит и замыкание \( A \), поскольку \( \text{Cl}(A) \) является наименьшим замкнутым множеством, включающим \( A \).
• Если A ⊆ B, то Cl(A) ⊆ Cl(B)
  Включение множеств сохраняется при переходе к замыканиям: из \( A \subseteq B \) следует \( \text{Cl}(A) \subseteq \text{Cl}(B) \).
• Множество A замкнуто тогда и только тогда, когда A = Cl(A)
  Множество является замкнутым в точности тогда, когда оно совпадает со своим замыканием, то есть содержит все свои предельные точки.
• Замыкание множества равно объединению множества и его предельных точек
  Если \( A' \) обозначает множество предельных точек множества \( A \), то $$ \text{Cl}(A) = A \cup A' $$
• Идемпотентность
  Повторное применение операции замыкания не изменяет результат: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$
• Включённость множества в своё замыкание
  Любое множество всегда содержится в своём замыкании: $$ A \subseteq \text{Cl}(A) $$

Продолжение следует.