Открытые множества

Множество A называется открытым, если для каждой точки x из A (x∈A) существует окрестность точки x, целиком лежащая внутри данного множества.

 

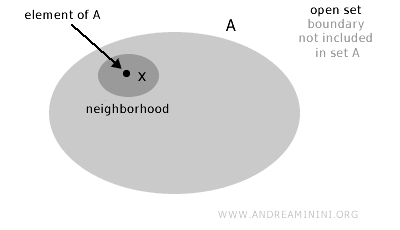
Проще говоря, множество считается открытым, если его «граница» не входит в него.

С формальной точки зрения множество A в топологическом пространстве X является открытым, если для любой точки x из A существует окрестность x, полностью содержащаяся в A.

Note. Это означает, что вокруг каждой точки множества можно выбрать область, которая целиком лежит внутри множества и не касается его границы.

Практический пример

Самый простой пример открытого множества на прямой - открытый интервал.

What is an open interval? Открытым интервалом на \( \mathbb{R} \) называют множество всех действительных чисел \( x \), для которых выполняется \( a < x < b \), где \( a \) и \( b \) - действительные числа, причем \( a < b \).

Такое множество обозначают (a,b). Круглые скобки показывают, что точки a и b не принадлежат множеству.

Например, интервал (3,10) является открытым множеством на числовой прямой.

В этом случае множество A содержит бесконечно много чисел между 3 и 10, не включая границы.

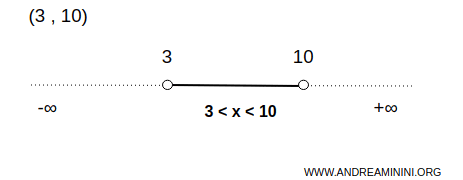
Это означает, что для любой точки x внутри интервала можно подобрать небольшой открытый интервал вокруг нее, который полностью будет лежать внутри (3,10).

Например, для точки x=3.1 можно выбрать интервал (3.09,3.11), который полностью содержится в (3,10).

То же верно для любой другой точки интервала (3,10), поскольку между любыми двумя действительными числами лежит бесконечно много других чисел.

Note. Даже для точки, очень близкой к границе, например 3.001, можно построить окрестность вида 3.001±0.00000001, которая все равно будет целиком лежать в интервале (3,10) и содержать бесконечно много чисел.

Это наглядный одномерный пример открытого множества.

Другие примеры

Теперь перенесем идею на двумерное пространство, например на координатную плоскость.

Рассмотрим множество точек внутри окружности радиуса r=1 с центром в начале координат (0;0).

$$ x^2+y^2<1 $$

Это неравенство описывает множество всех точек, расстояние от которых до центра меньше 1. Такие точки лежат внутри окружности и не включают ее границу.

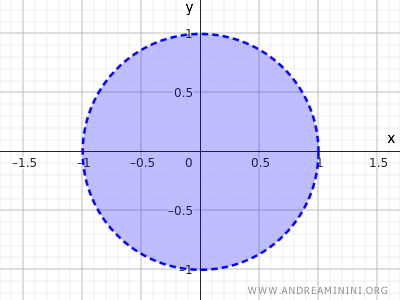
Это еще один пример открытого множества.

Когда множество является замкнутым?

Чтобы множество стало замкнутым, достаточно включить в него точки на границе окружности.

$$ x^2+y^2 \le 1 $$

В этом случае условие про окрестности уже не выполняется для всех точек.

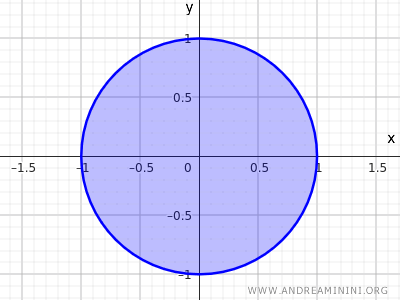
Для замкнутого множества точки на окружности не имеют окрестности, полностью лежащей внутри множества.

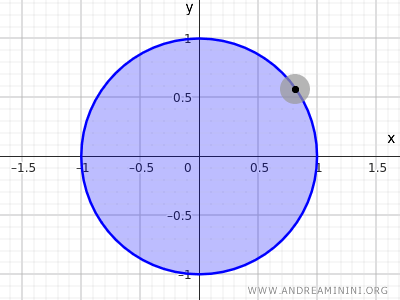
Note. В топологии множество, заданное уравнением $ x^2+y^2=1 $, не является ни открытым, ни замкнутым в пространстве R², так как оно содержит только граничные точки и не включает внутренние. Множество, заданное неравенством $ x^2+y^2<1 $, является открытым, потому что содержит все внутренние точки. Если же рассматривать множество $ x^2+y^2\le 1 $, включая и границу, то оно будет замкнутым.

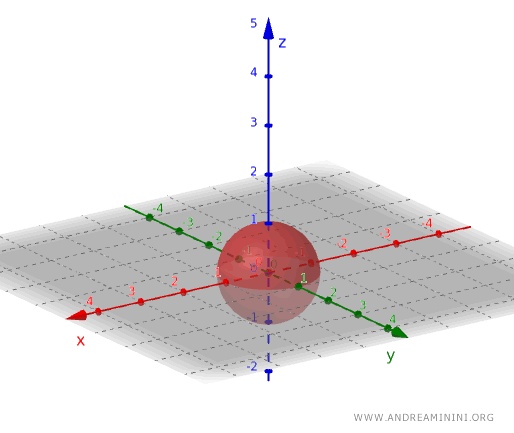
Аналогичный пример существует и в трехмерном пространстве: множество точек внутри сферы при условии, что точки на поверхности не входят в него, будет открытым.

Выбор топологии

Открытые интервалы удобны и наглядны, поэтому они хорошо передают основную идею.

Но понятие открытого множества значительно шире и не сводится только к интервалам или похожим фигурам.

Поняв основные примеры, полезно рассмотреть более общий подход.

Понятие открытости множества зависит от выбранной для пространства топологии.

Ключевая идея в том, что определение открытого множества может меняться в зависимости от топологии.

В одной топологии множество может быть закрытым, а в другой - открытым.

Иными словами, любое множество может оказаться открытым, если так определяет выбранная топология.

What is a topology? Топология на пространстве - это семейство множеств, объявленных открытыми, которое удовлетворяет определенным аксиомам. В частности, объединение любого количества открытых множеств должно быть открытым, а пересечение конечного количества открытых множеств также должно быть открытым.

Поэтому не стоит ограничиваться только привычными примерами вроде интервалов или кругов.

В топологии понятие открытости гораздо шире, чем может показаться на интуитивных примерах.

Практический пример

Рассмотрим пространство \( \{a, b\} \), состоящее всего из двух элементов.

На нем можно определить как минимум две разные топологии: тривиальную и дискретную.

• Тривиальная топология
  В тривиальной топологии на \( \{a, b\} \) открыты только два множества: пустое \( \emptyset \) и само пространство \( \{a, b\} \). Это самая «бедная» топология без дополнительной структуры.
• Дискретная топология
  В дискретной топологии открыты все подмножества \( \{a, b\} \). То есть открыты \( \{a\} \), \( \{b\} \), \( \{a, b\} \) и \( \emptyset \). Такая топология является самой «насыщенной», так как открытыми считаются любые множества.

Теперь посмотрим на множество \( \{a\} \) с точки зрения обеих топологий:

• В тривиальной топологии множество {a} не является открытым
  Единственное непустое открытое множество - это \( \{a, b\} \).
• В дискретной топологии множество {a} открыто
  В этой топологии любой поднабор \( \{a, b\} \), включая \( \{a\} \) и \( \{b\} \), является открытым по определению.

Таким образом, множество \( \{a\} \) будет открытым в дискретной топологии и не будет открытым в тривиальной.

Этот пример показывает, насколько определение открытости множества зависит от выбранной топологии.

Теорема об открытых множествах

Теорема 1

Пусть задано топологическое пространство (X,T), где X - множество, а T - топология на нем. Подмножество S⊂X является открытым в (X,T) тогда и только тогда, когда для каждой точки s∈S существует окрестность U, целиком содержащаяся в S, то есть U⊂S.

По определению множество S открыто, поскольку оно включено в топологию T и принадлежит пространству (X,T).

Иначе говоря, каждую точку s∈S можно рассматривать как внутреннюю точку множества, поскольку она обладает окрестностью, полностью лежащей в S.

Следовательно, окрестность U_s любой точки s∈S является открытым множеством, которое не выходит за пределы S.

$$ x \in U_s \subset S \subset X $$

Любое открытое множество может быть представлено как объединение открытых окрестностей своих точек.

Значит, если для каждой точки s∈S существует окрестность U_s⊂S, то множество S является открытым, поскольку оно образуется как объединение таких окрестностей.

Иными словами, множество является открытым тогда и только тогда, когда для каждой его точки существует окрестность, полностью содержащаяся в этом множестве.

Example. Представьте стол, на котором рассыпаны стеклянные шарики. Каждый шарик - это точка множества. Говоря, что множество «открыто», мы утверждаем, что вокруг каждого шарика можно свободно провести окружность так, чтобы она не выходила за край стола. Если для любого шарика можно начертить окружность, полностью лежащую внутри стола, то множество шариков будет «открытым». Смысл открытости в том, что у каждой точки есть «запас пространства», целиком принадлежащий тому же множеству.

Теорема 2

Пусть задано множество \( X \) и базис \( B \) топологии на \( X \). Подмножество \( A \subset X \) является открытым в топологии, порожденной \( B \), тогда и только тогда, когда для каждой точки \( x \in A \) существует базисный элемент \( B_x \in B \), содержащий точку \( x \) и целиком лежащий в \( A \), то есть \( B_x \subseteq A \).

Эта теорема отражает ключевое свойство топологий, задаваемых через базис.

Проще говоря, каждая точка множества \( A \) должна иметь «локальную окрестность» \( B_x \), принадлежащую базису и не выходящую за пределы \( A \).

Тем самым подтверждается, что множество \( A \) действительно является открытым в топологии, определенной базисом \( B \).

Proof. Если множество A открыто в топологии, порожденной базисом B, то по определению оно представимо как объединение базисных множеств. Следовательно, любая точка x из A принадлежит некоторому базисному множеству B_x, полностью содержащемуся в A. Обратное рассуждение также справедливо: если каждая точка множества A лежит хотя бы в одном базисном множестве B_x, которое целиком содержится в A, то A является открытым множеством в топологии, порожденной B.

Example

Рассмотрим множество \( X = \{1, 2, 3, 4, 5\} \) и базис топологии \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \). Определим, является ли множество \( A = \{1, 2, 3\} \) открытым.

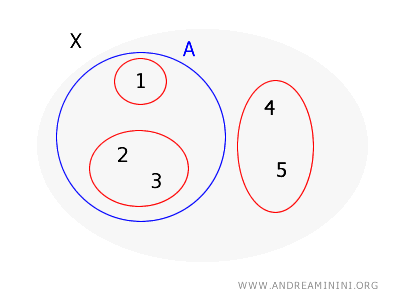
Для каждой точки множества \( A \) необходимо найти базисное множество, которое содержит эту точку и целиком лежит внутри \( A \):

• Для точки \( 1 \) подходит базисное множество \( \{1\} \).
• Для точки \( 2 \) подходит базисное множество \( \{2, 3\} \), полностью входящее в \( A \).
• Для точки \( 3 \) также подходит \( \{2, 3\} \).

Каждая точка множества \( A \) содержится в базисном элементе, лежащем внутри \( A \), а значит, выполняется условие теоремы.

Итак, \( A \) является открытым множеством в топологии, определенной базисом \( B \).

Example 2

Возьмем те же \( X = \{1, 2, 3, 4, 5\} \) и \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \).

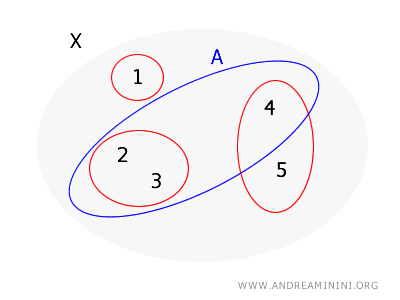
Проверим, является ли множество \( A = \{2, 3, 4\} \) открытым.

• Для точки \( 2 \) можно взять \( \{2, 3\} \), которая лежит в \( A \).
• Для точки \( 3 \) подходит то же множество \( \{2, 3\} \).
• Для точки \( 4 \) подходящего базисного элемента нет, потому что единственное множество, содержащее 4, это \( \{4, 5\} \), которое выходит за пределы \( A \).

Следовательно, множество \( A \) не является открытым в топологии, порожденной \( B \), так как не для каждой точки найдется базисное множество, целиком лежащее внутри \( A \).

Замечания

Несколько полезных фактов об открытых множествах

• Множество A является открытым тогда и только тогда, когда A = Int(A)
  Множество \( A \) в топологическом пространстве \( X \) является открытым тогда и только тогда, когда оно совпадает со своей внутренностью, то есть является объединением всех открытых множеств, содержащихся в \( A \). $$ A = \text{Int}(A) $$

И так далее.