Открытый шар

Открытый шар, обычно называемый в математике открытой окрестностью точки, это множество всех точек, расположенных на расстоянии меньше некоторого радиуса r от фиксированной точки c, которую принимают за центр. $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Такой объект рассматривают в метрическом пространстве \( M \), где метрика \( d \) задает расстояние между точками и подчиняется стандартным аксиомам. Благодаря метрике можно строго определять, какие точки находятся ближе друг к другу, а какие дальше.

Открытый шар полностью определяется двумя величинами: центром и радиусом. Другими словами, зная точку c и число r, мы точно знаем, какие точки входят в шар.

Когда говорят, что шар является открытым, имеют в виду следующее простое, но важное свойство: в любой точке внутри шара можно построить еще один, меньший открытый шар, который полностью помещается внутри исходного. Это ключевой элемент топологической структуры.

Замечание: открытые шары сохраняют свои свойства при масштабировании и переносах. Если увеличить или уменьшить их размер или переместить в другое место, они по-прежнему остаются открытыми шарами в топологическом смысле.

Рассмотрим для наглядности плоскость R². Чтобы найти расстояние между точкой p = (x, y) и точкой c = (x₀, y₀), принятой за центр, используют классическую евклидову формулу.

$$ d(p,c) = \sqrt{(x-x_0)^2 + (y-y_0)^2} $$

Открытые окрестности на плоскости имеют фундаментальное значение. Именно на их основе формируется стандартная топология R², которая служит отправной точкой для изучения топологических пространств.

Стандартная топология на R² представляет собой систему всех возможных открытых шаров.

$$ B = \{ B(p, r) \ | \ p \in R^2, \ r > 0 \} $$

Здесь p это любая точка плоскости, а r это радиус соответствующей окрестности.

Хотя для плоскости можно задать и другие топологии, именно стандартная используется чаще всего, поскольку она согласуется с естественной геометрической интуицией.

Для любой точки $ q \in B(p,r) $ всегда существует число \( \epsilon > 0 \), такое что открытый шар B(q, \epsilon) целиком содержится внутри B(p,r). Это свойство отражает внутреннюю согласованность структуры метрических пространств.

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ such \ that \ B(q,\epsilon) \subset B(p,r) $$

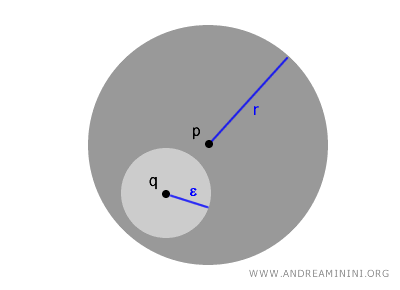
Так создается иерархия вложенных открытых шаров, которая лежит в основе многих идей топологии.