Нормальное топологическое пространство

Топологическое пространство $ X $ называют нормальным, если выполняются два ключевых условия.

Каждое одноточечное множество замкнуто
Это означает, что для любой точки $ x \in X $ множество $\{x\}$ рассматривается как замкнутое в данной топологии.
Любые два непересекающихся замкнутых множества можно разделить открытыми множествами
Если замкнутые множества $ A $ и $ B $ не имеют общих точек, то можно подобрать открытые множества $ U $ и $ V $, которые содержат соответственно $ A $ и $ B $ и не пересекаются между собой.

Идея нормальности проста и интуитивна. Если два замкнутых множества не пересекаются, то в нормальном пространстве их можно «разнести» так, чтобы каждое оказалось внутри собственного открытого множества. Это свойство делает структуру пространства особенно удобной для построения непрерывных функций, отличающих одно множество от другого.

Пример
Дополнительные сведения

Пример

Возьмем пространство $ X = \mathbb{R} $ со стандартной топологией, где открытые множества формируются из интервалов $ (a, b) $.

Рассмотрим два замкнутых множества, которые не пересекаются.

$ A = \{0\} $, одноточечное множество.
$ B = [2, 3] $, замкнутый отрезок.

Оба множества замкнуты и полностью отделены друг от друга. На рисунке это хорошо видно.

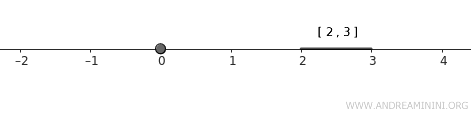
example

Примечание. Множество $ A $ состоит всего из одной точки и автоматически является замкнутым. Множество $ B $ представляет собой замкнутый отрезок, а такие множества всегда замкнуты в стандартной топологии на $ \mathbb{R} $.

Наша задача состоит в том, чтобы найти два открытых множества, содержащих $ A $ и $ B $ и не пересекающихся друг с другом.

Для $ A = \{0\} $ подойдет интервал $ U = (-1, 1) $.

$$ A \subset U = (-1,1) $$

Для множества $ B = [2,3] $ можно взять интервал $ V = (1, 4) $, который полностью покрывает его.

$$ B \subset V = (1,4) $$

Эти интервалы не пересекаются, поскольку между ними остается свободное пространство. Тем самым мы получаем конкретный пример нормальности на прямой.

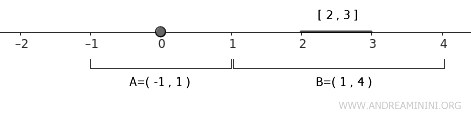
example

Тот же подход работает для любых непересекающихся замкнутых множеств в $ \mathbb{R} $. Для каждого такого случая можно подобрать открытые множества, которые разделяют их.

Таким образом, стандартная топология на $ \mathbb{R} $ является нормальной.

Дополнительные сведения

Вот несколько важных фактов, которые помогают лучше понять нормальные пространства.

$ \mathbb{R} $ со стандартной топологией действительно нормально
Оно удовлетворяет не только условию регулярности, но и более сильному условию нормальности, что делает пространство особенно удобным для анализа.
Каждое метрическое пространство является нормальным
Это следует из свойств метрики, позволяющих ясно отделять множества с помощью открытых шаров.
Любое нормальное пространство обязательно регулярно
Нормальность включает в себя регулярность, так что первое является более сильным свойством.

Эти особенности делают нормальные пространства важным объектом в топологии.