Пересечение внутренностей множеств
Пересечение внутренностей двух множеств \(A\) и \(B\) совпадает с внутренностью их пересечения \( \text{Int}(A \cap B) \) $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
Это утверждение выражает важное и интуитивно понятное свойство внутренности в топологии. Если сначала взять внутренние части множеств \(A\) и \(B\), а затем пересечь их, результат будет тем же самым, что и внутренняя часть множества \(A \cap B\).
Говоря проще, внутренние точки, общие для \(A\) и \(B\), образуют ровно внутренность их пересечения.
Чтобы уверенно понимать это свойство, достаточно чётко представлять себе два базовых понятия:
- Внутренность множества (\(\text{Int}(A)\)). Это совокупность всех точек множества \(A\), для каждой из которых существует открытая окрестность, полностью лежащая в \(A\).
- Пересечение (\(\cap\)). Это множество элементов, принадлежащих одновременно и \(A\), и \(B\).
Именно поэтому пересечение внутренностей \(\text{Int}(A)\) и \(\text{Int}(B)\) не даёт ничего лишнего и не теряет ни одной точки по сравнению с внутренностью множества \(A \cap B\).
Наглядный пример
Представим два круга \(A\) и \(B\), которые частично перекрываются.
Внутренность каждого круга включает все его точки, за исключением границы. Это стандартное представление внутренности в евклидовой топологии.
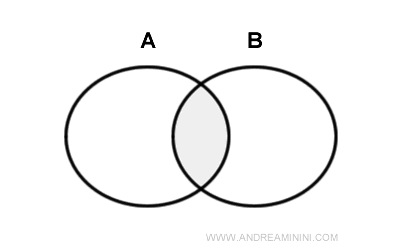
Если рассмотреть пересечение внутренних областей этих кругов, мы получим внутреннюю часть той области, где множества \(A\) и \(B\) пересекаются.
Доказательство
Доказательство удобно разбить на два логически симметричных шага.
1] Первое включение (\(\subseteq\))
Пусть точка принадлежит внутренности множества \(A\) и одновременно внутренности множества \(B\). Это означает, что вокруг неё существуют открытые окрестности, полностью содержащиеся соответственно в \(A\) и в \(B\).
Их пересечение также является открытым множеством и целиком лежит в \(A \cap B\). Следовательно, данная точка принадлежит внутренности множества \(A \cap B\).
Пусть \(x \in \text{Int}(A) \cap \text{Int}(B)\). Тогда \(x \in \text{Int}(A)\) и \(x \in \text{Int}(B)\).
По определению внутренности существуют открытые окрестности \(U\) и \(V\) такие, что \(x \in U \subseteq A\) и \(x \in V \subseteq B\).
Рассмотрим множество \(W = U \cap V\). Так как \(U\) и \(V\) открыты, множество \(W\) также является открытым и содержит точку \(x\).
Кроме того, \(W \subseteq A \cap B\).
Следовательно, \(x \in \text{Int}(A \cap B)\).
Отсюда следует включение \(\text{Int}(A) \cap \text{Int}(B) \subseteq \text{Int}(A \cap B)\).
2] Второе включение (\(\supseteq\))
Теперь предположим, что точка принадлежит внутренности множества \(A \cap B\). Тогда существует открытая окрестность этой точки, полностью лежащая в пересечении \(A\) и \(B\).
Это автоматически означает, что та же окрестность содержится и в \(A\), и в \(B\). Следовательно, точка является внутренней для каждого из этих множеств.
Пусть \(x \in \text{Int}(A \cap B)\). Тогда существует открытая окрестность \(W\) точки \(x\), такая что \(W \subseteq A \cap B\).
Из этого следует, что \(W \subseteq A\) и \(W \subseteq B\).
Следовательно, \(x \in \text{Int}(A)\) и \(x \in \text{Int}(B)\).
Тем самым получаем включение \(\text{Int}(A \cap B) \subseteq \text{Int}(A) \cap \text{Int}(B)\).
Поскольку доказаны оба включения, можно сделать окончательный вывод:
\[ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) \]
Доказательство завершено.
И так далее.