Хаусдорфово пространство

Хаусдорфово пространство это топологическое пространство, где любые две различные точки можно отделить непересекающимися открытыми окрестностями. Такое свойство делает структуру пространства более предсказуемой и удобной для анализа.

Если сформулировать кратко, то для любых точек $ x $ и $ y $ найдутся открытые множества $ U $ и $ V $ такие, что $ U \cap V = \emptyset $. Каждая точка получает собственную область, не пересекающуюся с областью другой точки.

Это условие задаёт чёткую «геометрию отделимости» и напоминает привычную картину расстояний в обычном евклидовом пространстве.

Хаусдорфовы пространства особенно важны в современной математике. В них корректно устроена сходимость последовательностей, что делает работу с такими пространствами гораздо более надёжной.

Одно из ключевых свойств состоит в том, что одноточечные множества всегда замкнуты, ведь их дополнения открыты.

Примеры
Замечания

Примеры

Пример 1. Стандартная топология на прямой

Рассмотрим стандартную топологию на числовой прямой $\mathbb{R}$.

example of the real number line

В этой топологии отдельные точки не являются открытыми. Чтобы множество было открытым, оно должно содержать целый интервал вокруг каждой своей точки. Одноточечное множество не может этому соответствовать.

Пояснение: между любыми двумя вещественными числами лежит бесконечно много других. Поэтому множество вроде $ \{x\} $ не может содержать интервал и не считается открытым.

Но его дополнение всегда открыто, значит само одноточечное множество замкнуто.

the neighborhood of the single point is an open set

Эта же топология является хаусдорфовой. Для любых двух точек $ a $ и $ b $ можно подобрать интервалы, которые не пересекаются.

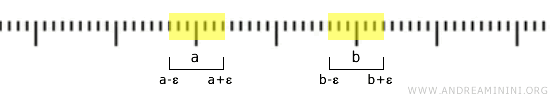
neighborhoods of points a and b

Если $ a < b $, достаточно выбрать интервалы $ (a-\epsilon, a+\epsilon) $ и $ (b-\epsilon, b+\epsilon) $ с таким $ \epsilon $, что $ a+\epsilon < b-\epsilon $.

Пример 2. Дискретная топология

Теперь посмотрим на пространство X = {1, 2, 3} с дискретной топологией, где открытыми считаются все подмножества.

Открытыми будут:

$ \emptyset $
$ \{1\}, \{2\}, \{3\} $
$ \{1,2\}, \{1,3\}, \{2,3\} $
$ \{1,2,3\} $

Такое пространство всегда хаусдорфово, ведь любые две точки можно развести одноточечными окрестностями.

Например, U={1} и V={2} не пересекаются:

$$ \{1\} \cap \{2\} = \emptyset $$

Одноточечные множества: открытые или замкнутые?

В дискретной топологии они одновременно открытые и замкнутые. Это связано с тем, что открыты все подмножества, а их дополнения тоже открыты.

Например, в X={1,2,3} множество {1} открыто, и его дополнение {2,3} также открыто, значит {1} замкнуто.

Открытые: любая точка образует открытое множество.
Замкнутые: дополнение X/{x} открыто, значит {x} замкнуто.

Итак, каждое одноточечное множество в дискретной топологии открыто и замкнуто одновременно.

Главная разница между дискретной и стандартной топологиями состоит в том, что в стандартной топологии открыты только те множества, которые действительно являются окрестностями всех своих точек.

Замечания

Сходимость в хаусдорфовых пространствах

В хаусдорфовом пространстве у сходящейся последовательности может быть только один предел. Если бы последовательность имела два разных предела, их окрестности неизбежно пересекались бы, что противоречит определению хаусдорфовости.

Краткое доказательство. Если почти все члены последовательности лежат в окрестности A точки x и одновременно почти все лежат в окрестности B точки y, то $ A \cap B \neq \emptyset $. В хаусдорфовом пространстве такое невозможно, поэтому предел единственный.

И далее можно рассматривать другие свойства хаусдорфовых пространств.