Топология подпространства

Пусть есть топологическое пространство \( (X, T) \), где \( X \) это множество, а \( T \) семейство открытых множеств. Если взять подмножество \( Y \subseteq X \), то на нём вводится топология подпространства. Она определяется так: \[
T_Y = \{ U \cap Y \mid U \in T \}, \] то есть открытыми в \( Y \) считаются все пересечения открытых множеств пространства \( X \) с самим \( Y \). Эту топологию также называют индуцированной.

Иными словами, множество \( V \subseteq Y \) открыто в подпространстве тогда и только тогда, когда существует открытое множество \( U \subseteq X \) такое, что \( V = U \cap Y \).

Отсюда следует: каждое открытое множество подпространства имеет вид \( U \cap Y \), а каждое замкнутое множество имеет вид \( C \cap Y \), где \( U \) открыто, а \( C \) замкнуто в \( X \).

Таким образом, топологическое подпространство это подмножество пространства \( X \) с топологией, унаследованной от исходной.

Примечание. Открытые множества подпространства \( Y \) не обязаны быть открытыми в \( X \). Возможны различные варианты: множество может быть открытым в \( Y \), но замкнутым в \( X \), или наоборот. Есть множества, которые открыты или замкнуты одновременно и в \( Y \), и в \( X \). Также встречаются клопены, то есть множества, являющиеся и открытыми, и замкнутыми.

Пример

Возьмём пространство \( \mathbb{R} \) со стандартной топологией, где открытыми считаются открытые интервалы. Рассмотрим подмножество \( Y = [0, 1] \).

Топология подпространства на \( Y \) включает множества вида:

$$ U \cap [0, 1] $$

где \( U \) открыто в \( \mathbb{R} \).

Например, интервал (-1, 0.5) открыт в \( \mathbb{R} \).

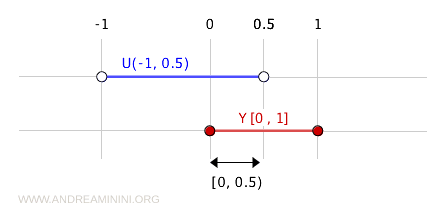
Его пересечение с \( Y \) даёт:

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

Интервал \( [0, 0.5) \) не является открытым в \( \mathbb{R} \), но является открытым в подпространстве \( Y \). Это важный момент: в подпространстве открытость определяется исключительно тем, как множество получается пересечением с \( Y \).

Теперь рассмотрим замкнутый интервал [-1, 0.5] в \( X \). Его пересечение с \( Y \):

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

Значит, множество \( [0, 0.5] \) замкнуто в подпространстве \( Y \).

Примечание. Интервалы [0,a) и (a,1], где 0

Некоторые множества открыты и в \( X \), и в \( Y \), например (0.2, 0.8). Аналогично, есть множества, замкнутые в обоих пространствах, например [0.2, 0.8].

Особый случай это само множество \( Y = [0, 1] \). Оно является и открытым, и замкнутым в своей топологии.

• Открытость
  Чтобы увидеть, что \( [0, 1] \) открыто в подпространстве, берём \( U = \mathbb{R} \). Тогда:
  $$ \mathbb{R} \cap [0, 1] = [0, 1] $$
• Замкнутость
  Чтобы убедиться, что \( [0, 1] \) замкнуто, берём замкнутое множество \( C = [0, 1] \) в \( \mathbb{R} \):
  $$ C \cap Y = [0, 1] $$

  Примечание: Дополнение множества \( [0,1] \) в самом \( Y \) пусто, а пустое множество всегда открыто. Это ещё один аргумент в пользу того, что \( [0,1] \) замкнуто.

Таким образом, интервал \( [0, 1] \) в топологии подпространства одновременно открыт и замкнут. Такие множества называют клопенами.

Пример 2

Рассмотрим стандартную топологию на множестве действительных чисел \(\mathbb{R}\). В этой структуре любое множество вида (a, b), где \( a < b \), является открытым.

Теперь посмотрим на множество целых чисел \(\mathbb{Z}\). Его можно рассматривать как подпространство \(\mathbb{R}\), потому что каждое одноточечное множество \(\{n\}\) получается как пересечение подходящего открытого интервала на прямой с множеством \(\mathbb{Z}\). Это напрямую следует из определения индуцированной топологии.

Например:

$$ (6.5, 7.5) \cap \mathbb{Z} = \{ 7 \} $$

То же самое работает для любого целого числа. Отсюда следует важный вывод: каждое одноточечное множество в \(\mathbb{Z}\) открыто. А если открыта каждая точка, значит открыто и любое подмножество \(\mathbb{Z}\), ведь оно является объединением одноточечных множеств.

Например:

$$ (5.5, 8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

Именно поэтому индуцированная топология на \(\mathbb{Z}\) совпадает с дискретной топологией.

Примечание. Дискретная топология на \(\mathbb{Z}\) формально является самостоятельной топологией. Однако индуцированная топология, полученная от стандартной топологии на \(\mathbb{R}\), полностью ей эквивалентна.

Пример 3

Теперь рассмотрим трёхмерное пространство \(\mathbb{R}^3\) со стандартной топологией, где открытые множества задаются объединениями открытых шаров. Пусть \( S^2 \) это единичная сфера:

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

Топология подпространства на \( S^2 \) определяется простым правилом: множество открыто на сфере, если его можно представить как пересечение \( S^2 \) с некоторым открытым множеством в \(\mathbb{R}^3\).

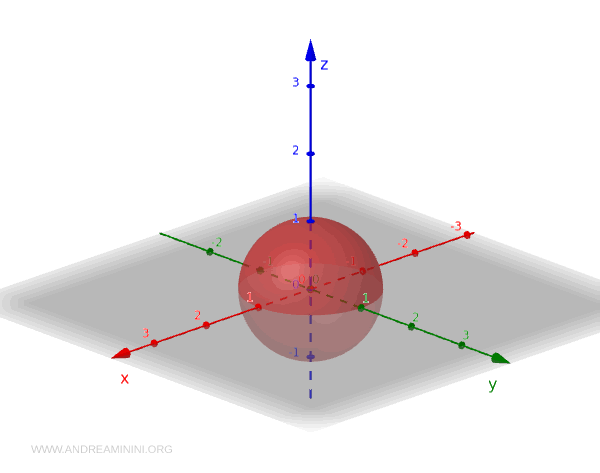
Несколько показательных примеров:

• Пересечение с внешней открытой областью
  Возьмём множество \( U = \{ x^2 + y^2 + z^2 < 2 \} \). Его пересечение со сферой даёт всю сферу:
  $$ U \cap S^2 = S^2 $$ Так как каждая точка на сфере удовлетворяет равенству \( x^2 + y^2 + z^2 = 1 \), а это меньше 2. Следовательно, сфера открыта в собственной индуцированной топологии.
• Открытая часть сферы
  Рассмотрим множество всех точек сферы с \( z > 0 \). Оно также может быть записано как пересечение сферы с подходящим открытым множеством в \(\mathbb{R}^3\), поэтому верхняя полусфера открыта в индуцированной топологии.
• Основные операции
  Пустое множество и сама сфера всегда открыты. Конечное пересечение открытых множеств остаётся открытым. То же верно и для произвольных объединений.

Таким образом, сфера \( S^2 \), будучи подпространством \(\mathbb{R}^3\), наследует топологическую структуру окружающего пространства. Открытые множества на сфере это пересечения открытых множеств \(\mathbb{R}^3\) со сферой.

Свойства индуцированной топологии

Индуцированная топология обладает несколькими фундаментальными свойствами, важными для понимания работы подпространств:

1. Открытые множества
   Любое открытое множество в \( Y \) имеет форму \( U \cap Y \), где \( U \) открыто в \( X \).
2. Пустое множество и всё пространство
   Пустое множество и всё \( Y \) всегда открыты, поскольку:
   \( \emptyset = \emptyset \cap Y \),
   \( Y = X \cap Y \).
3. Конечные пересечения
   Пересечение любого конечного количества открытых множеств в \( Y \) остаётся открытым.
4. Произвольные объединения
   Объединение произвольного семейства открытых множеств всегда открыто.

Дополнительные замечания

Некоторые важные наблюдения о поведении подпространств:

• Стандартная топология на подмножестве \( Y \subseteq \mathbb{R}^n \) всегда совпадает с индуцированной топологией, полученной от \(\mathbb{R}^n\).

• Пример. Пусть \( Y = [-1,0) \cup (0,1] \subset \mathbb{R} \). В стандартной топологии на \( Y \) интервалы [-1,0) и (0,1] открыты, поскольку являются пересечениями \( Y \) с открытыми интервалами прямой:
  $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Стандартная топология на \( Y \) полностью совпадает с индуцированной. Оба множества являются клопенами, поскольку их дополнения также открыты и замкнуты в рамках пространства \( Y \).

• Теорема о базисе индуцированной топологии
  Если \( B_X \) это базис топологии на \( X \), то семейство \( B_Y = \{ B \cap Y \mid B \in B_X \} \) образует базис индуцированной топологии на \( Y \).

Эти свойства лежат в основе изучения подпространств и позволяют глубже понять, как топологические структуры наследуются и изменяются при переходе к подмножествам.