Топология

Топология - это раздел математики, который изучает свойства пространств, сохраняющиеся при непрерывных деформациях, таких как растяжение, изгиб или скручивание, при условии, что объект не разрывается и не склеивается.

Иными словами, топология интересуется теми геометрическими свойствами, которые остаются неизменными при любых непрерывных преобразованиях.

Такие свойства могут измениться только в результате разрывных действий, например при разрыве части пространства или при склеивании двух его фрагментов.

Классический пример: сфера и куб топологически эквивалентны, поскольку одну фигуру можно непрерывно превратить в другую без разрывов и склеиваний.

Сфера и тор, напротив, топологически неэквивалентны, так как для перехода от одной фигуры к другой необходимо создать или устранить отверстие, а это неизбежно связано с разрывом или склеиванием.

Таким образом, топология сосредоточена на устройстве и связности пространств, а не на точных метрических характеристиках, таких как расстояние, размер или форма.

В топологическом подходе длина, площадь, объём или угловые меры не имеют принципиального значения. Гораздо важнее качественные свойства фигур и возможность их взаимного преобразования с помощью непрерывных деформаций.

К таким свойствам относятся, например, связность, компактность, число отверстий у объекта и другие глобальные характеристики пространства.

Топология вводит понятие топологического пространства, а ключевыми преобразованиями в ней являются гомеоморфизмы - взаимно однозначные непрерывные отображения с непрерывным обратным, которые деформируют пространство, сохраняя его топологическую структуру.

Поэтому топологию часто называют «геометрией резинового листа»: объекты мысленно представляют изготовленными из упругого материала, который можно растягивать, изгибать или сжимать, но нельзя разрывать или склеивать. Это одна из фундаментальных и объединяющих областей современной математики.

История

Возникновение топологии относят к XVIII веку.

Её истоки связаны с задачей о семи мостах Кёнигсберга, предложенной Леонардом Эйлером. Рассматривая этот, казалось бы, чисто практический вопрос, Эйлер заложил основы понятий связности и топологических структур.

Эта задача стала отправной точкой для исследования свойств пространств, не зависящих от измерений и расстояний, и фактически положила начало топологии как самостоятельной дисциплине.

Задача о семи мостах: в речном городе остров соединён с берегами семью мостами. Можно ли пройти по каждому мосту ровно один раз, не повторяя переходов?

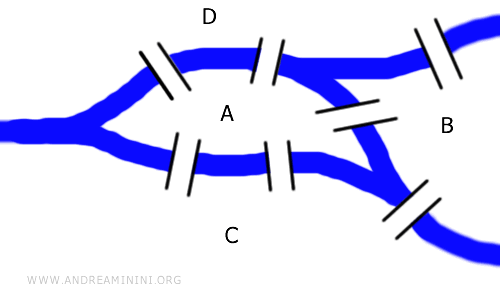
Решение этой задачи не требует знания длин мостов или расстояний между ними - это по сути топологическая задача, которую удобно представить в виде графа. Показанный ниже граф топологически эквивалентен исходной схеме мостов.

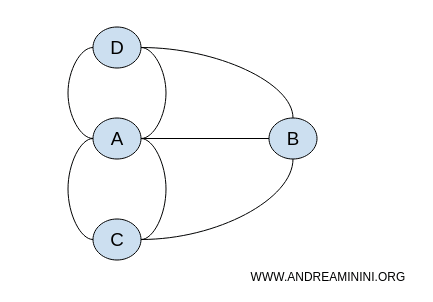
Точное расположение узлов не имеет значения - важны только связи между ними. Поэтому одну и ту же задачу можно представить бесконечным числом топологически эквивалентных графов.

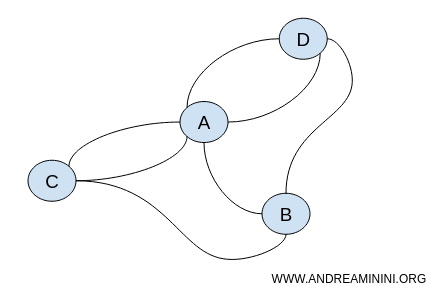
Все эти графы обладают одними и теми же топологическими свойствами - непрерывностью и связностью.

Эйлер показал, что задача о семи мостах - не геометрическая в обычном смысле, поскольку не связана с измерениями. Он доказал её неразрешимость, тем самым заложив основы новой области - «геометрии положения».

В XIX веке идеи Эйлера получили развитие в работах Карла Фридриха Гаусса, Августа Мёбиуса, Иоганна Листинга, Бернгарда Римана и Феликса Клейна, которые исследовали свойства форм и поверхностей с топологической точки зрения.

Примечание: термин «топология» впервые ввёл Иоганн Листинг в 1847 году, хотя широкое распространение он получил лишь спустя несколько десятилетий.

В то же время «геометрия положения» нашла применение в практических задачах - например, при анализе электрических цепей, чему способствовали работы Густава Кирхгофа.

Позднее, на рубеже XIX и XX веков, Анри Пуанкаре внёс решающий вклад в становление топологии, создав основы алгебраической топологии.

В XX веке топология оформилась как обширная область с несколькими направлениями - алгебраическим, общим, дифференциальным и геометрическим. Среди её основателей - Феликс Хаусдорф, Георг Кантор и Лёйтзен Брауэр.

Сегодня топология - одна из центральных дисциплин математики, изучающая свойства, сохраняющиеся при непрерывных деформациях.

Современная топология охватывает широкий спектр подходов и методов: от строго абстрактных до прикладных. Её можно рассматривать как общее исследование форм и пространств на самом фундаментальном уровне.

Несмотря на свою абстрактность, топологические концепции применяются во множестве реальных задач - в экономике, инженерии, анализе данных и естественных науках.

Топологические пространства

Топологическое пространство - это множество X с заданной на нём структурой T, называемой «топологией». Она задаёт общий язык для описания непрерывности, близости и пределов в более широком смысле, чем традиционная геометрия или анализ.

$$ (X,T) $$

Пример: классическим примером топологического пространства является прямая действительных чисел \( \mathbb{R} \) со стандартной топологией. Множество считается открытым, если оно содержит некоторый интервал вокруг каждой своей точки. Такая структура позволяет по-новому рассматривать непрерывность и пределы - уже в топологическом контексте.

Гомеоморфизмы

Гомеоморфизм - это непрерывное взаимно-однозначное отображение между двумя топологическими пространствами, обратное к которому также непрерывно. Такое преобразование сохраняет все основные топологические свойства объектов.

Если между двумя пространствами существует гомеоморфизм, они считаются топологически эквивалентными.

Пример: превращение кофейной чашки в бублик - классический пример гомеоморфизма. Оба объекта имеют одно отверстие, и один можно непрерывно преобразовать в другой без разрывов и склеиваний, сохранив их топологическую сущность.

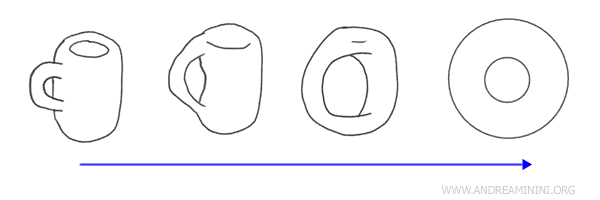
Геометрия и топология

Геометрия и топология - разные, но тесно связанные области математики. Каждая исследует пространственные свойства с разных сторон.

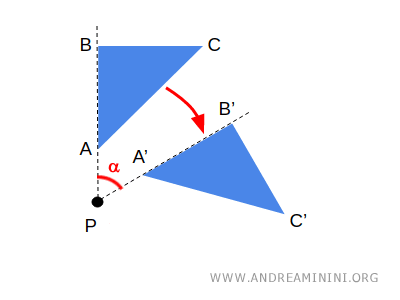
• Геометрия изучает свойства, связанные с расстояниями, углами и размерами фигур, сосредотачиваясь на количественных соотношениях. Примером является вращение фигуры - геометрическое преобразование, при котором длины сторон сохраняются.
  

  Классическая евклидова геометрия - наиболее известная, однако неевклидовы геометрии исследуют последствия изменения или отрицания пятого постулата Евклида о параллельных прямых.

• Топология фокусируется на свойствах, которые сохраняются при непрерывных деформациях - растяжении, сжатии или изгибе без разрывов и склеиваний. Она рассматривает качественные характеристики, такие как непрерывность, связность и «гибкость» форм. Например, если куб из глины постепенно сплющить до сферы, он сохранит непрерывность и связность - это пример топологического преобразования.
  

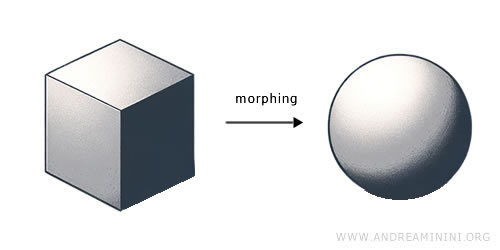
  Пример: куб из пластилина можно преобразовать в сферу, просто деформируя его без добавления или удаления материала. Такое преобразование является гомеоморфизмом - базовым типом топологических преобразований.
  

Несмотря на различия, геометрия и топология тесно взаимосвязаны: топология нередко рассматривается как обобщение геометрии, расширяющее её рамки до более абстрактных структур.

Топология изучает не количественные, а структурные, инвариантные свойства пространств, выходя за пределы традиционной геометрии.

Разделы топологии

Топология охватывает множество направлений, каждое из которых исследует особые аспекты топологических пространств и имеет свои методы и области применения.

• Геометрическая топология: изучает свойства, сохраняющиеся при непрерывных деформациях - растяжении, сжатии, изгибе - без разрывов и склеиваний. Здесь рассматриваются такие понятия, как связность, компактность и границы без использования метрики.
• Общая топология (или топология множеств точек): исследует топологические пространства в самом общем виде, изучая понятия открытых и замкнутых множеств, непрерывности, компактности и связности, а также метрические и функциональные пространства.
• Алгебраическая топология: применяет алгебраические методы к изучению топологических пространств, устанавливая связь между топологическими и алгебраическими структурами для более глубокого понимания их свойств.
• Дифференциальная топология: использует дифференциальное исчисление для изучения свойств топологических пространств, локально подобных евклидову пространству. Это позволяет вводить понятия касательных, гладкости и дифференцируемости.
• Прикладная топология: занимается использованием топологических методов за пределами чистой математики - в анализе данных, теории сетей, инженерии, биологии и вычислительных науках.

Каждое направление топологии обладает собственным подходом и методологией, что подчёркивает широту и универсальность топологических идей.