Замкнутые множества
Множество B в топологическом пространстве X называется замкнутым, если для любого элемента из дополнения u∈X-B существует окрестность, целиком лежащая в дополнении X-B.
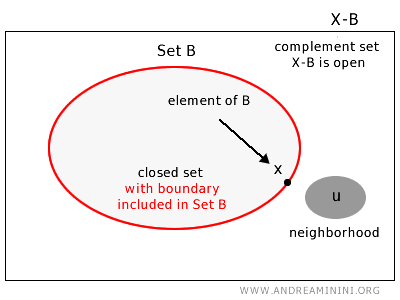
Иначе говоря, множество является замкнутым, если все его граничные точки принадлежат ему самому.
Строгое определение формулируется так: множество B в топологическом пространстве X считается замкнутым, если его дополнение X-B является открытым множеством.
Примечание: Это означает, что в замкнутом множестве B всегда найдутся точки, для которых невозможно выбрать окрестность, полностью лежащую внутри B.
Практический пример
Рассмотрим числовую прямую R и замкнутый отрезок.
Что такое замкнутый отрезок? Замкнутым отрезком на R называется множество всех точек x, удовлетворяющих условию a≤x≤b, где a и b - действительные числа, a
Отрезок обозначают символом [a,b]. Квадратные скобки указывают на то, что точки a и b включены в множество.
Например, отрезок [3,10] является замкнутым множеством на числовой прямой R.
В этом случае множество B содержит бесчисленное множество точек между 3 и 10 включительно.
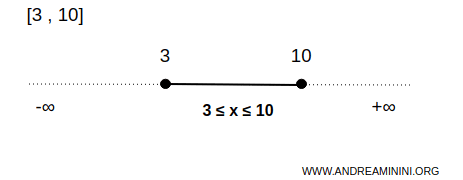
Это означает, что в множество входят все точки x, удовлетворяющие условию 3≤x≤10, включая обе границы.
Однако не для каждой точки на этом отрезке существует окрестность, целиком лежащая внутри него.
Например, любая окрестность левой граничной точки x=3 выходит за пределы отрезка [3,10].
Примечание: Даже бесконечно малая окрестность, например 3±0.00000001, не будет полностью принадлежать отрезку [3,10], поскольку 3-0.00000001 меньше 3. Та же ситуация возникает и для правой границы x=10. Для этих точек невозможно подобрать окрестность, целиком лежащую в [3,10].
Этот пример иллюстрирует замкнутое множество в одномерном случае.
Другие примеры замкнутых множеств
Аналогичное рассуждение верно и для двумерного случая, то есть для плоскости.
Рассмотрим множество точек внутри и на границе круга радиуса r=1 с центром в начале координат (0,0).
$$ x^2+y^2≤1 $$
Это неравенство задаёт множество всех точек, расстояние которых от начала координат не превышает 1. В него входят и точки окружности, и точки внутренней области круга.
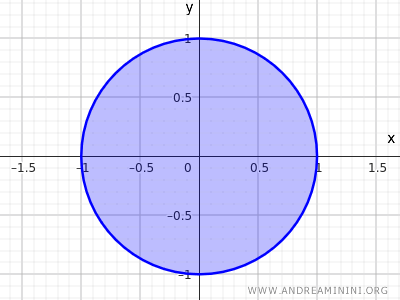
Это ещё один пример замкнутого множества.
Нетрудно заметить, что точки, лежащие на окружности, не обладают окрестностями, целиком содержащимися внутри множества.
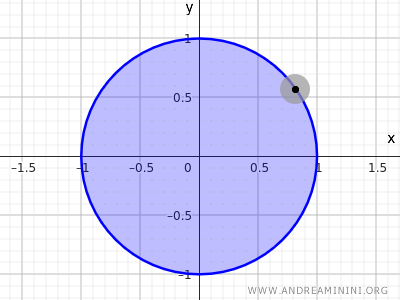
Примечание: В топологии множество, заданное уравнением $ x^2+y^2=1 $, не является ни открытым, ни замкнутым в евклидовом пространстве R2, так как оно включает только точки окружности и не содержит внутренней области. Напротив, множество, заданное неравенством $ x^2+y^2≤1 $, является замкнутым, поскольку содержит и внутренние точки, и граничные.
По тому же принципу понятие замкнутого множества переносится в трёхмерное пространство (шар), а затем и в n-мерные пространства (n-сферы).
Дополнение замкнутого множества
В пространстве X дополнение замкнутого множества C является открытым множеством и обозначается X-C.
Если множество C замкнуто в X, то его дополнение X-C автоматически будет открытым.
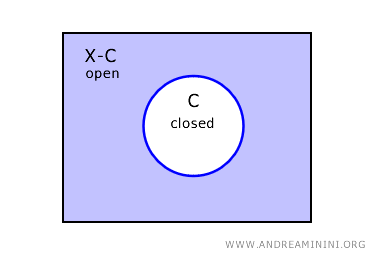
И наоборот, если множество U является открытым, то его дополнение X-C будет замкнутым в X.
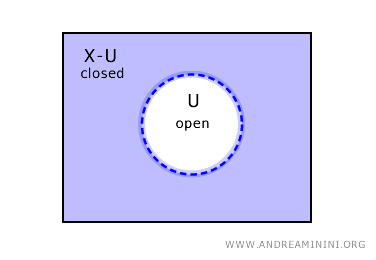
Это ещё не все возможные случаи. В топологических пространствах встречаются также множества, одновременно являющиеся открытыми и замкнутыми, а также множества, не принадлежащие ни к одному из этих классов.
Иными словами, если множество не является замкнутым, это не означает, что оно обязательно открыто, и наоборот.
Пример
Рассмотрим топологию T на множестве X={a,b,c,d}, состоящем из четырёх элементов.
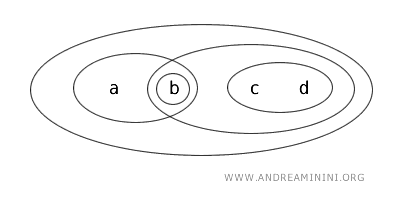
В этой топологии открыты следующие множества: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, Ø.
Проанализируем их:
- {b} - открытое множество, так как оно прямо указано в определении топологии.
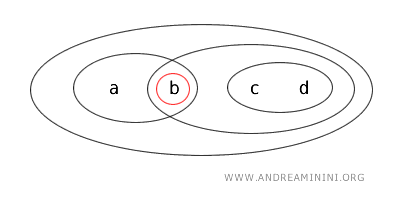
- {a} - замкнутое множество, поскольку оно является дополнением к открытому множеству X-{b,c,d}={a}, где X={a,b,c,d}.
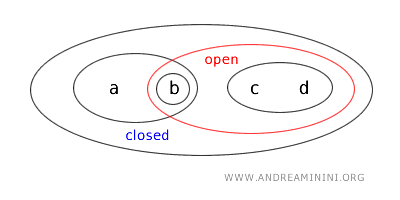
- {a,b} - множество, являющееся одновременно открытым и замкнутым. Такое множество называют «clopen». В обычной топологии на ℝ подобные случаи редки, но в общем случае топологических пространств они возможны. Здесь {a,b} является открытым по определению топологии T и замкнутым, так как оно дополняет открытое множество X-{c,d}.
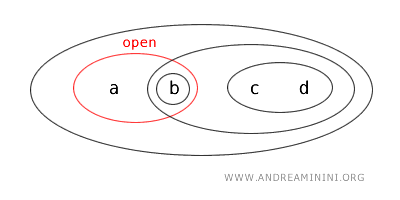
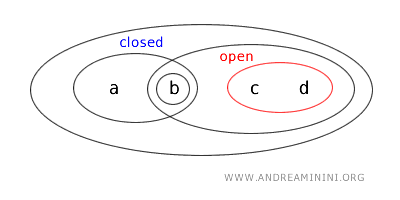
- {b,c} - множество, не являющееся ни открытым, ни замкнутым. Оно не удовлетворяет критериям открытости и не является дополнением к открытому множеству.
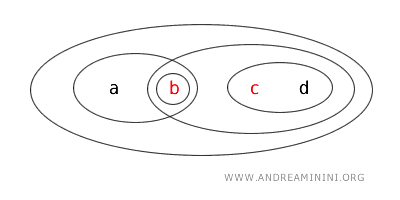
Этот пример показывает, что в одной и той же топологии могут встречаться открытые множества, замкнутые множества, множества, обладающие обоими свойствами, и множества, не относящиеся ни к одному из этих типов.
Свойства замкнутых множеств
Замкнутое множество определяется как дополнение к открытому множеству. Ему присущи следующие фундаментальные свойства:
- Пустое множество (Ø) и всё пространство X по определению являются замкнутыми.
- Пересечение произвольного семейства замкнутых множеств всегда является замкнутым множеством.
- Объединение конечного числа замкнутых множеств также образует замкнутое множество.
Пример:
В стандартной топологии евклидова пространства Rn любое одноточечное множество является замкнутым.
На прямой R1 дополнение к множеству {n} состоит из всех точек, отличных от n.
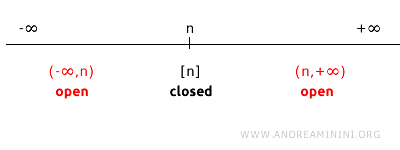
Это дополнение можно представить как объединение двух открытых интервалов: (-∞, n) ∪ (n, +∞).
Поскольку интервалы (-∞, n) и (n, +∞) открыты в стандартной топологии, их объединение также является открытым множеством.
Следовательно, раз дополнение множества {n} открыто, само множество {n} замкнуто.
Важный момент: не каждое одноточечное множество является замкнутым в любой топологии. Всё зависит от того, какие множества считаются открытыми. Например, рассмотрим иную топологию на R, порождённую интервалами вида (n, n+1) для всех целых n. В такой топологии отдельные точки не являются замкнутыми, поскольку не содержат своих граничных точек.
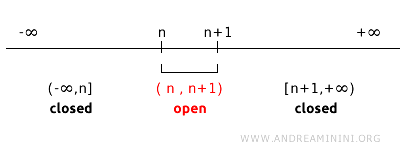
Так, множества (1,2) и (2,3) считаются открытыми. Их дополнения имеют вид (-∞, 1] ∪ [2, +∞) и (-∞, 2] ∪ [3, +∞). Поэтому невозможно получить дополнение, совпадающее с одноточечным множеством {2}. В целом, для любого интервала (n, n+1) его дополнение представлено в виде объединения двух замкнутых полуинтервалов (-∞, n] ∪ [n+1, +∞). Таким образом, в этой топологии отдельные точки не являются замкнутыми, что подчёркивает зависимость определения замкнутости от выбора топологии.
Пояснения и дополнительные замечания
Ниже приведены полезные наблюдения, расширяющие понимание темы.
- Замкнутые множества и их предельные точки
Предельная точка множества - это точка, в любой окрестности которой содержится, помимо неё самой, хотя бы одна точка множества. Замкнутые множества характеризуются тем, что они включают все свои предельные точки, в то время как открытые множества могут их не содержать.Пример: Замкнутый отрезок [0,1] на числовой прямой включает все свои предельные точки. Например, для точки 0.5 любая окрестность содержит бесчисленное множество точек из [0,1].
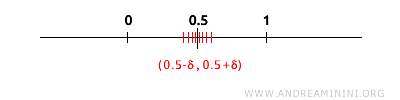
То же верно и для граничных точек. Например, точка 0 является предельной, поскольку всякая окрестность 0 содержит точки интервала: 0.1, 0.01, 0.001 и так далее.
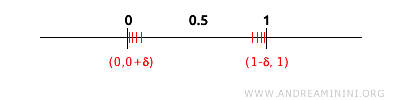
Итак, любая точка замкнутого интервала [0,1] окружена окрестностями, содержащими другие точки множества. - Множество A замкнуто тогда и только тогда, когда A = Cl(A)
В топологическом пространстве множество \( A \) является замкнутым тогда и только тогда, когда оно совпадает со своим замыканием, то есть \( A = \text{Cl}(A) \). Замыкание множества включает все его точки вместе с предельными точками. Если множество содержит все свои предельные точки, оно замкнуто по определению.
И так далее.