Стандартная топология на вещественной прямой

Стандартная топология на множестве R устанавливает, что каждый открытый интервал (a, b), где a < b, а также любое конечное или бесконечное объединение таких интервалов считаются открытыми множествами.

Проще говоря, множество U считается открытым, если для каждой его точки x существует открытый интервал (a, b), содержащий эту точку и полностью лежащий в пределах U.

$$ x \in (a,b) \subseteq U $$

То есть каждая точка открытого множества U находится внутри некоторого интервала (a, b), который также принадлежит этому множеству.

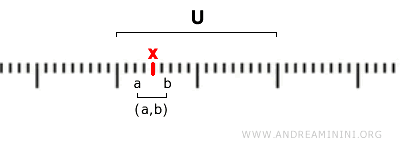
В стандартной топологии к открытым множествам относятся следующие случаи:

• Открытые интервалы
  В стандартной топологии на \( \mathbb{R} \) открытыми считаются интервалы \( (a, b) \), где a < b, а также любые их объединения, независимо от того, конечные они или бесконечные.
• Операции с множествами
  Открытые множества сохраняют свои свойства при объединении и конечных пересечениях.
  • Объединения: объединение любого количества открытых множеств всегда остаётся открытым.
  • Конечные пересечения: пересечение ограниченного числа открытых множеств также является открытым.

Стандартная топология - это лишь один из возможных способов описания структуры множества X. Она называется «стандартной» из-за своей фундаментальной роли и широкого применения в математике.

Эта топология выбрана потому, что она наглядно выражает привычные интуитивные представления о близости, открытости и непрерывности, особенно на вещественной прямой R.

Примечание: другие топологии на R или на других множествах могут иметь другие базисы. Это означает, что понятие открытого множества может определяться по иным правилам. Подобные топологии создаются, чтобы исследовать особые свойства или рассматривать новые математические ситуации.

Пример

Базой стандартной топологии на вещественной прямой R является совокупность всех открытых интервалов (a, b), где a < b.

$$ B = \{ (a,b) \subset; R \ | \ a \lt b \} $$

Для любой точки x внутри интервала всегда можно найти меньший интервал, который полностью содержится в исходном. Это свойство и делает множество открытым в стандартной топологии.

$$ \forall \ x \ \in U \ \exists \ \epsilon>0 \ | \ x \in (x-\epsilon, x+\epsilon) \subseteq U $$

Здесь U - открытое множество в стандартной топологии на R. Эта топология используется чаще всего, поэтому и получила название «стандартной».

Интервал (0, 1)

Рассмотрим интервал (0,1) без концов 0 и 1 и применим к нему стандартную топологию.

Проверим, образует ли он топологическое пространство.

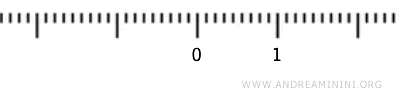
Подмножество \( U \subset (0, 1) \) считается открытым, если для каждой точки \( x \in U \) существует интервал \( (a, b) \) в \( \mathbb{R} \), такой что \( x \in (a, b) \) и \( (a, b) \cap (0, 1) \subseteq U \).

Сам интервал (0,1) можно рассматривать как пересечение открытых множеств стандартной топологии на R.

Следовательно, интервал \( (0, 1) \) является топологическим пространством с топологией, индуцированной стандартной топологией на \( \mathbb{R} \).

Например, множества \( (0.1, 0.5) \), \( (0.2, 0.9) \) или их объединение \( (0.1, 0.5) \cup (0.6, 0.8) \) - все они открыты в \( (0, 1) \) относительно индуцированной топологии. Иными словами, открытые множества внутри \( (0, 1) \) - это те, что уже открыты в R, но ограничены самим интервалом \( (0, 1) \).

Так как \( (0, 1) \) - подпространство \( \mathbb{R} \), оно сохраняет все основные свойства топологического пространства.

Конечное множество

Рассмотрим конечное множество X={1,2,3}, состоящее из трёх целых чисел.

Можно ли считать его топологическим пространством в стандартной топологии на \( \mathbb{R} \)?

Отдельные элементы X не образуют открытых множеств, потому что стандартная топология на \( \mathbb{R} \) основана на интервалах, а не на отдельных точках множества \( X \).

Если рассматривать элемент {2} как вещественное число, он входит в интервал (2-ε, 2+ε), но этот интервал содержит и другие точки, не принадлежащие X. Следовательно, определение открытого множества стандартной топологии на R здесь не выполняется.

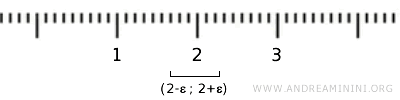
Если рассматривать \( X \) как подмножество \( \mathbb{R} \) и использовать «индуцированную топологию» или «топологию подпространства», то открытыми будут только пустое множество и всё множество \( X \). Такое пространство малоинтересно для анализа.

Для конечных множеств, например \( X \), чаще применяют дискретную топологию, где любое подмножество \( X \) считается открытым по определению.

Таким образом, стандартная топология играет ключевую роль при изучении свойств вещественной прямой и служит основой для понимания более сложных топологических структур.