Путём связные пространства

Путём связным называется топологическое пространство S, в котором любые две точки A и B можно соединить непрерывной линией, не выходя за пределы самого пространства.

Представьте себе обычный лист бумаги и забудьте о его краях.

Он образует непрерывную поверхность, открытую область без границ.

На таком листе вы легко сможете провести линию от точки A до точки B, не отрывая ручку от бумаги. Это и есть интуитивный пример путём связного пространства.

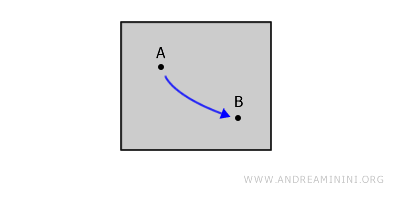
Главная идея проста: путь между точками A и B целиком лежит внутри той области, к которой они принадлежат.

Любое путём связное пространство автоматически является связным.

Это звучит логично - если пространство разорвано на отдельные части, провести непрерывный путь между точками, находящимися в разных частях, уже невозможно.

Но вот интересный момент: обратное утверждение неверно. Связное пространство не обязательно будет путём связным.

Рассмотрим пример, который кажется странным, но в математическом смысле совершенно корректен.

Пусть заданы два множества Q и T:

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ 0 \} $$

Множество Q состоит из всех точек синусоиды, определённой для всех действительных чисел, кроме нуля. В нуле функция не существует, потому что деление на ноль невозможно.

Множество T - это просто одна точка в начале координат.

Если построить график функции sin(1/x), можно увидеть, что волны бесконечно сгущаются к нулю. То есть множества Q и T бесконечно близки друг к другу, но не пересекаются.

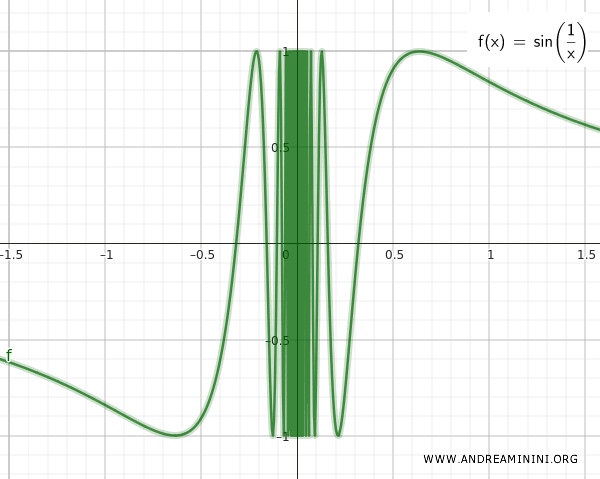
Теперь рассмотрим объединение этих множеств:

$$ S = Q \cup T $$

Множество S является связным, потому что для любой окрестности точки 0, как бы мала она ни была, в ней всегда найдутся точки множества Q.

Это связано с тем, что ноль является точкой сгущения функции sin(1/x).

Однако множество S не является путём связным. Не существует непрерывного пути, который мог бы соединить любую точку множества Q с нулём из множества T, не выходя за пределы S.

Замечание: Для функции f(x)=1/x ситуация другая. Здесь множества Q и T явно раздельны и не приближаются друг к другу.

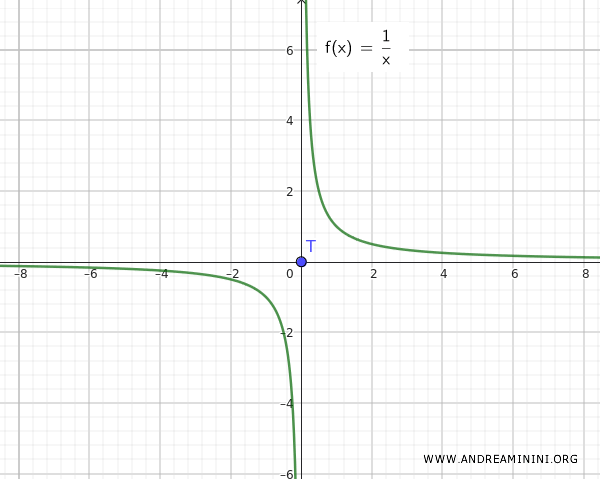
Этот пример показывает, что объединение связного множества Q={∀ x ∈ R-{0}, 1/x} и изолированной точки T={0} не образует связного множества, если только эта точка (в нашем случае 0) не является точкой сгущения.

 Таким образом, в топологии путём связность - понятие более строгое, чем просто связность.