Множества, одновременно открытые и замкнутые

Множество в заданной топологии называется «одновременно открытым и замкнутым», если оно удовлетворяет определениям как открытого, так и замкнутого множества.

Иными словами, такое множество в рассматриваемой топологии обладает обеими характеристиками одновременно.

Термин отражает объединение двух понятий: «открытое множество» и «замкнутое множество».

Подобные множества сочетают свойства открытых множеств и замкнутых множеств.

Такая ситуация возможна тогда, когда и множество, и его дополнение являются открытыми в одной и той же топологии.

Примечание: В топологии на множестве действительных чисел такие примеры встречаются редко, тогда как в других топологических пространствах они могут возникать довольно часто. Эти множества особенно интересны, поскольку позволяют лучше понять структуру и свойства топологического пространства.

Пример

Рассмотрим множество X={a,b,c,d} с топологией T.

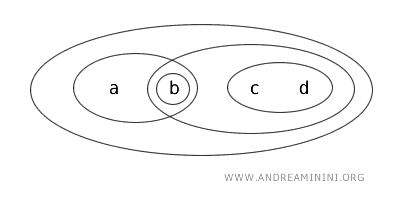
В этой топологии открыты следующие множества: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, Ø.

Отсюда следует, что подмножество {a,b} является открытым множеством в топологии T.

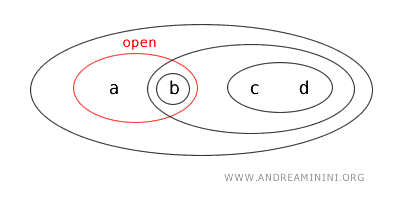
При этом множество {a,b} является дополнением открытого множества {c,d}:

$$ X - \{ c,d \} = \{a , b \} $$

Поскольку дополнение открытого множества всегда является замкнутым,

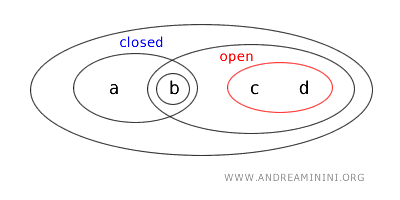
множество {a,b} одновременно является и замкнутым множеством.

Таким образом, в топологии T множество {a,b} обладает обоими свойствами одновременно.

Пустое множество и всё множество

В любой топологии на множестве X пустое множество (∅) и всё множество (X) всегда одновременно являются открытыми и замкнутыми.

Множество считается «одновременно открытым и замкнутым», если в рамках данной топологии оно удовлетворяет определениям открытого и замкнутого множества.

Для наглядности напомним ключевые определения.

Согласно определению открытого множества, пустое множество (∅) и всё множество (X) всегда являются открытыми.

Согласно определению замкнутого множества, множество замкнуто тогда, когда открыто его дополнение.

Объединяя эти два утверждения, получаем:

• Пустое множество (∅)
  Пустое множество по определению открыто. В то же время оно замкнуто, так как его дополнение $ X \setminus ∅=X $ является открытым. Следовательно, оно обладает обоими свойствами.
• Всё множество (X)
  Множество X по определению открыто. Оно также замкнуто, поскольку его дополнение $ X \setminus X=∅ $ является открытым. Таким образом, X одновременно открыто и замкнуто.

Следовательно, в любой топологии множество X и пустое множество ∅ всегда обладают этим свойством.

И так далее.