Простосвязные пространства в топологии

Простосвязным называют топологическое пространство, в котором любой замкнутый контур можно непрерывно стянуть в одну точку.

Проще говоря, если любую петлю внутри пространства можно плавно «сжать» до точки, не выходя за его пределы, то такое пространство простосвязно.

Это означает, что пространство представляет собой единое целое - без внутренних пустот или отверстий.

Важно: любое простосвязное пространство обязательно связно. Но не каждое связное пространство является простосвязным.

Пример: сфера и тор

Хорошим примером простосвязного пространства служит сфера. Любую замкнутую линию на её поверхности можно плавно стянуть в точку, не покидая поверхность.

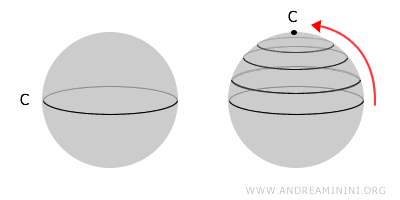
Совсем другое дело - тор, знакомый многим по форме «пончика». Из-за центрального отверстия не все контуры на торе можно стянуть до точки, поэтому он не является простосвязным.

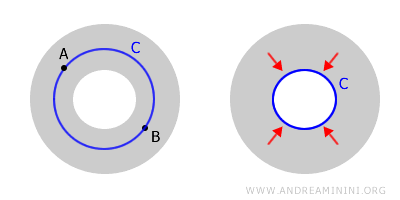
Таким образом, связность пространства не всегда означает простосвязность.

Тор остаётся связным пространством, ведь любые две точки на нём можно соединить непрерывным путём, не выходя за его пределы.

Однако он не простосвязен, потому что некоторые замкнутые кривые невозможно стянуть в точку из-за «дырки» в центре.

Если пространство связно, но не простосвязно, его называют многосвязным. Примеры - кольцевая область и тороидальное пространство.

Итак, простосвязность - это более сильное условие, чем связность по дугам.

Это понятие играет важную роль во многих областях математики и физики, где форма и структура пространства определяют его фундаментальные свойства.