Связность в топологии: как понять, что пространство едино

В топологии пространство называют связным, если его нельзя разделить на два непересекающихся открытых множества. Проще говоря, связность показывает, можно ли соединить любые две точки внутри пространства непрерывным путём, не покидая его границы.

Это понятие лежит в самом сердце топологии, потому что помогает понять, насколько «цельным» является пространство и каким образом его части взаимосвязаны между собой.

Это топологическое свойство, поскольку оно определяется через открытые множества.

Связность - это не просто абстрактная идея. Она помогает математикам и физикам описывать форму и структуру пространств, изучать, где они «рвутся», а где остаются едиными. Благодаря этому свойству можно классифицировать и сравнивать различные топологические объекты.

Простой пример

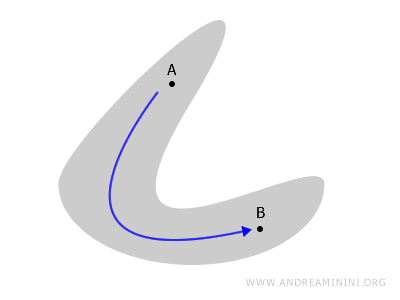
Представьте себе любую фигуру - например, плоский круг или поверхность многогранника. Если внутри неё можно провести непрерывную линию, соединяющую любые две точки A и B, и при этом линия не выходит наружу, то пространство связно.

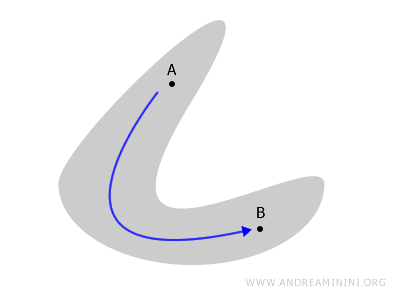
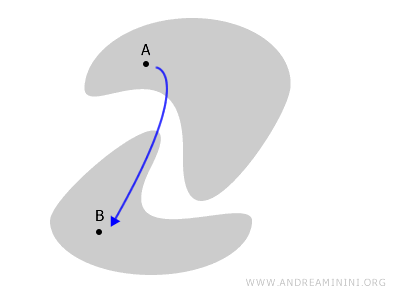
Если же фигура состоит из двух изолированных частей, между которыми нет пути, то такое пространство называется несвязным.

На рисунке ниже видно, что пространство разделено на две области: чтобы попасть из точки A в точку B, пришлось бы покинуть пределы самого пространства.

Когда пространство теряет связность

Самый наглядный пример - две комнаты, разделённые стеной. Каждая из них - открытое множество: оно не включает в себя стену и не пересекается с соседней областью.

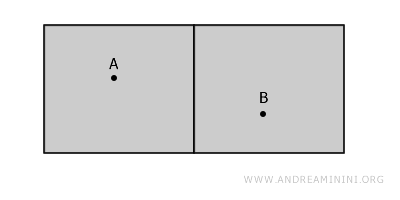
На первый взгляд кажется, что комнаты рядом, но они не связаны: чтобы пройти из точки A в точку B, нужно пересечь стену - выйти за пределы пространства.

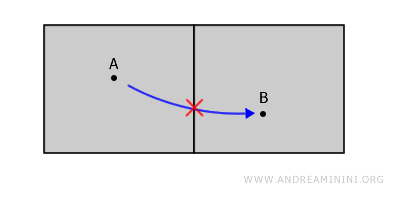
Из этого примера важно запомнить простое правило: границы не входят в состав открытых множеств.

Что такое локальная связность

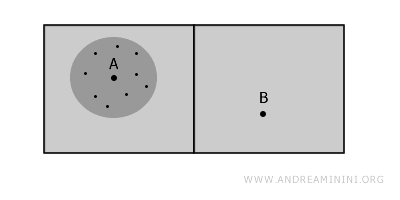
Локальная связность означает, что вокруг каждой точки пространства можно найти маленькое связное окружение. То есть, даже если всё пространство в целом несвязно, в окрестности каждой точки есть своя «цельная зона».

Например, возьмём всё те же две комнаты. В целом они не соединены, но внутри каждой из них все точки можно соединить между собой - это и есть пример локальной связности.

Два основных типа связности

В топологии выделяют два ключевых типа связности:

• Топологическая связность
  Топологическое пространство $ X $ называется связным, если его нельзя разделить на два непустых, непересекающихся открытых множества, объединение которых образует всё пространство. Иными словами, не существует способа «разделить» пространство на две независимые части.

  Пример. Интервал (-1, 1) является связным, тогда как объединение (-1, 0) ∪ (0, 1) - нет, поскольку здесь можно выделить два непустых, непересекающихся открытых множества (-1, 0) и (0, 1), которые вместе покрывают всё пространство.
  Эти множества образуют разделение данного пространства.

• Связность по пути (или по дуге)
  Пространство называется связным по пути, если для любых двух точек A и B в нём существует непрерывный путь, полностью проходящий внутри этого пространства. Каждое связное по пути пространство также является топологически связным, хотя обратное утверждение не всегда справедливо.

  Например, представьте себе замкнутую область на плоскости. Для любых двух точек A и B внутри неё можно провести непрерывную линию, не отрывая карандаша от бумаги и не выходя за пределы области.
  
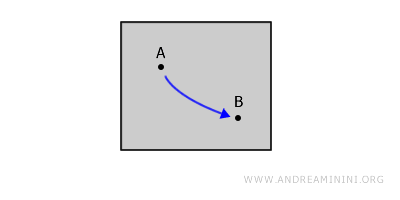
  Разница между связностью по пути и по дуге.  Связность по дуге во многом похожа на связность по пути, но путь в этом случае должен быть взаимно-однозначным - то есть не пересекаться сам с собой и не проходить через одну и ту же точку более одного раза.

• Простая связность
  Пространство называют просто связным, если любую замкнутую линию внутри него можно плавно «стянуть» до точки. Такое пространство не содержит отверстий или внутренних полостей. Просто связное пространство всегда связно, но обратное утверждение неверно.

  Сфера - классический пример просто связного пространства: любую петлю на её поверхности можно стянуть в точку. Тор (бублик) - нет, потому что отверстие мешает это сделать. Поэтому тор - связное, но не просто связное пространство.
  
  
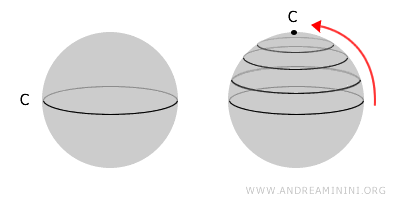
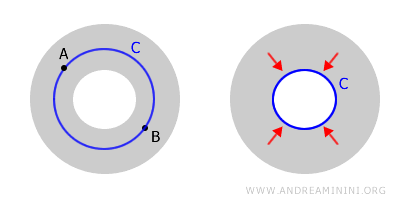
  Такое пространство называют многосвязным. Примером служит кольцевая область или поверхность тора.

Что стоит запомнить

• Связность помогает понять, где пространство едино, а где - разорвано.
• Локальная связность объясняет, почему части несвязного пространства могут быть цельными «на месте».
• На множестве действительных чисел связными являются только интервалы - простейший пример связного множества.