Неподвижные точки в топологии

В топологии неподвижной точкой называют значение, которое не меняется при применении к нему функции.

Если дана функция f(x), то точка p считается неподвижной, когда выполняется равенство f(p) = p. Иначе говоря, результат функции совпадает со входным значением.

$$ f(p) = p $$

Представьте поворот фигуры вокруг центра P.

Поворот меняет координаты всех точек фигуры в пространстве.

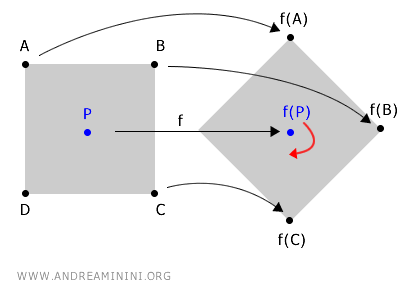
В этом случае точка P выступает как неподвижная, потому что функция поворота не изменяет её координаты.

$$ f(P) \longrightarrow P $$

Неподвижные точки встречаются гораздо чаще, чем может показаться. Они важны в численных методах, экономике, теории игр и других областях, где важно понять, к чему система приходит в состоянии равновесия.

Одним из ключевых результатов топологии, связанных с этой идеей, является теорема Брауэра о неподвижной точке.

Простой пример

Рассмотрим функцию f(x) = sin(x) на отрезке [0, 2π] радиан.

$$ f(x) = \sin(x) $$

Здесь легко заметить неподвижную точку при x = 0, поскольку sin(0) = 0.

$$ \sin(0) = 0 $$

В этом случае функция возвращает то же значение, которое получает на вход.

Пример 2

Теперь рассмотрим функцию f(x) = cos(x) на том же отрезке.

$$ f(x) = \cos(x) $$

Значение x = 0 здесь уже не подходит, потому что cos(0) = 1. Результат отличается от исходного значения, а значит, это не неподвижная точка.

Зато неподвижная точка существует при x ≈ 0.73908513

$$ \cos(0.73908513) = 0.73908513 $$

Это значение часто приводят как пример, потому что оно наглядно показывает, что неподвижные точки могут быть неочевидными и лежать между привычными нам числами.

Теорема Брауэра о неподвижной точке

Формулировка теоремы звучит так:

Для любой непрерывной функции, отображающей замкнутый n-мерный интервал в себя, существует хотя бы одна неподвижная точка.

Это теорема существования. Она не говорит, где именно находится неподвижная точка, но гарантирует, что она обязательно есть.

Эта идея широко используется для доказательства существования равновесия в экономике, биологии, динамических системах и многих других направлениях.

Дальнейшие примеры и обобщения показывают, насколько мощным может быть этот подход.