Регулярные топологические пространства
Топологическое пространство \( X \) называется регулярным, если выполняются следующие условия.
- Одноточечные множества замкнуты, то есть каждая точка в \( X \) образует замкнутое множество.
- Разделение точки и замкнутого множества. Для любой точки \( a \in X \) и любого замкнутого множества \( C \subset X \), не содержащего \( a \), существуют два открытых множества \( U \) и \( V \), не имеющие общих точек, такие что: \[ a \in U, \quad C \subset V, \quad U \cap V = \emptyset \]
В топологии регулярные пространства обладают более строгим свойством разделения, чем пространства Хаусдорфа.
Если регулярное пространство имеет счетную базу, то по теореме Урысона оно оказывается метризуемым.
Чем регулярность отличается от свойства Хаусдорфа?
Регулярное пространство гарантирует, что любую точку и замкнутое множество, которому она не принадлежит, можно разделить разными открытыми множествами. Это более сильное требование по сравнению со структурой Хаусдорфа, где достаточно разделять только две различные точки.
Примечание. Регулярность не совпадает с нормальностью. Нормальное пространство удовлетворяет более жесткому условию: любые два замкнутых множества, не имеющих общих точек, должны отделяться непересекающимися открытыми множествами. Поэтому каждое нормальное пространство является регулярным, но далеко не каждое регулярное пространство нормально.
Стоит помнить, что регулярность является всего лишь одним из вариантов аксиом разделения. Существуют регулярные пространства, которые не являются хаусдорфовыми, и наоборот. Эти свойства независимы друг от друга в общем случае.
Практический пример
Классический пример регулярного пространства это числовая прямая \( \mathbb{R} \) с привычной топологией.
Возьмем точку \( x \in \mathbb{R} \) и замкнутое множество \( C \), не содержащее эту точку.
Например, пусть \( x = 2 \), а замкнутое множество \( C \) имеет вид:
\[ C = (-\infty, 0] \cup [5, \infty) \]
Очевидно, \( x = 2 \notin C \), и множество \( C \) действительно замкнуто в стандартной топологии.
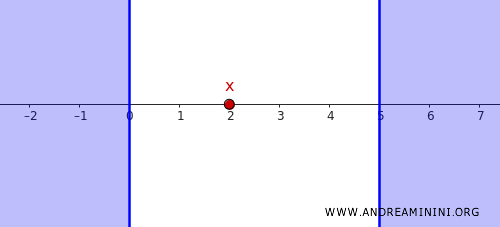
Теперь нам нужно построить два открытых множества, которые будут разделять \( x \) и \( C \).
Дополнение к \( C \) открыто, значит можно выбрать открытый интервал, содержащий точку \( x \).
Например, интервал \( (0,5) \) подходит, поскольку в него входит \( x = 2 \).
\[ (a, b) = (0, 5) \]
Выберем числа \( c \) и \( d \), между которыми находится точка \( x = 2 \).
\[ 0 < c < 2 < d < 5 \]
Например, можно взять \( c = 1 \) и \( d = 3 \).
Теперь определим два открытых множества.
- \( U = (c, d) = (1,3) \), оно содержит точку \( x = 2 \).
- \( V = (-\infty, c) \cup (d, \infty) = (-\infty, 1) \cup (3, \infty) \), оно охватывает все множество \( C \).
Эти множества не пересекаются, то есть \( U \cap V = \emptyset \), следовательно условие регулярности выполнено.
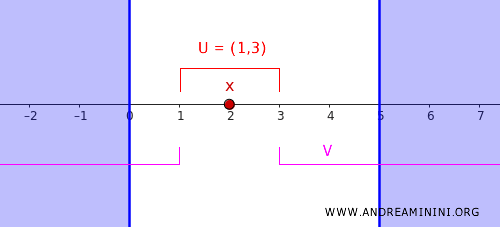
Таким образом, мы отделили точку \( x = 2 \) от замкнутого множества \( C \) с помощью открытых множеств \( U \) и \( V \). Это показывает, что числовая прямая с обычной топологией является регулярным топологическим пространством.
Заметки
Несколько пояснений и наблюдений о регулярных пространствах.
- Аксиомы разделения
В топологии свойства быть хаусдорфовым и быть регулярным включены в систему аксиом разделения. Эти аксиомы описывают, насколько тонко пространство различает точки и множества с помощью непересекающихся окрестностей , ключевая идея при изучении топологических структур.Примечание. Если говорить кратко, пространство является хаусдорфовым, когда любые две различные точки можно окружить непересекающимися открытыми окрестностями. Пространство является регулярным, если аналогичным образом можно отделить точку от замкнутого множества, которому она не принадлежит. Оба свойства показывают, насколько подробно топология различает элементы пространства , какова ее "разрешающая способность".
И так далее.