Объединение внутренностей двух множеств

Объединение внутренностей двух множеств $ A $ и $ B $ всегда содержится во внутренности их объединения: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \]. При этом равенство в общем случае не выполняется.

Это утверждение является базовым свойством топологии и помогает понять, как операция внутренности взаимодействует с объединением множеств.

Важно подчеркнуть, что речь идёт именно о включении. Совпадение этих множеств возможно лишь в отдельных случаях и не является универсальным правилом.

Иными словами, равенство

$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$

может выполняться, но на него нельзя рассчитывать в общем случае.

Практический пример

Рассмотрим два открытых интервала \( A \) и \( B \) на вещественной прямой \(\mathbb{R}\) со стандартной топологией:

$$ A = (0, 2), \qquad B = (1, 3) $$

Поскольку оба интервала открыты, их внутренности совпадают с самими интервалами:

$$ \text{Int}(A) = (0, 2), \qquad \text{Int}(B) = (1, 3) $$

Объединение внутренностей имеет вид:

$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) $$

Так как интервалы пересекаются, их объединение образует один интервал:

$$ (0, 2) \cup (1, 3) = (0, 3) $$

Объединение самих множеств также равно:

$$ A \cup B = (0, 3) $$

Внутренность объединения совпадает с этим интервалом:

$$ \text{Int}(A \cup B) = (0, 3) $$

В данном примере выполняется не только включение

$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B), $$

но и равенство. Однако это связано с конкретным взаимным расположением интервалов.

Рассмотрим теперь два замкнутых интервала $$ A = [0, 2], \qquad B = [2, 3] $$ Их внутренности равны $$ \text{Int}(A) = (0, 2), \qquad \text{Int}(B) = (2, 3) $$ Объединение множеств равно $ A \cup B = [0, 3] $, а его внутренность имеет вид $$ \text{Int}(A \cup B) = (0, 3) $$ Таким образом, включение $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ выполняется. Однако равенство отсутствует, поскольку точка $ 2 $ принадлежит внутренности объединения $$ 2 \in \text{Int}(A \cup B), $$ но не является внутренней ни для $ A $, ни для $ B $. Следовательно, $$ 2 \notin \text{Int}(A) \cup \text{Int}(B), $$ и потому $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B). $$ Этот пример ясно показывает, что включение может быть строгим.

Пример 2

Рассмотрим два непересекающихся открытых интервала:

$$ A = (0, 1), \qquad B = (2, 3) $$

Их внутренности совпадают с самими интервалами:

$$ \text{Int}(A) = (0, 1), \qquad \text{Int}(B) = (2, 3) $$

В этом случае объединение внутренностей равно объединению самих множеств:

$$ \text{Int}(A) \cup \text{Int}(B) = (0, 1) \cup (2, 3) $$

Внутренность объединения также имеет тот же вид:

$$ \text{Int}(A \cup B) = (0, 1) \cup (2, 3) $$

Здесь равенство выполняется, поскольку интервалы не соприкасаются и не создают новых внутренних точек.

Пример 3

Перейдём к примеру в двумерном пространстве \(\mathbb{R}^2\) со стандартной топологией.

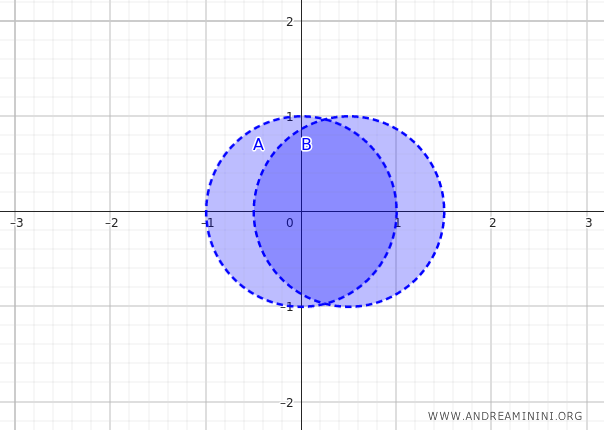
Пусть множества \( A \) и \( B \) представляют собой два открытых круга радиуса 1 с центрами в точках \( (0, 0) \) и \( (0.5, 0) \), которые частично перекрываются:

$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$

$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0.5)^2 + y^2 < 1 \} $$

Так как оба множества открыты, их внутренности совпадают с самими множествами:

$$ \text{Int}(A) = A, \qquad \text{Int}(B) = B $$

Следовательно, объединение внутренностей совпадает с объединением множеств:

$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$

Внутренность объединения также совпадает с этой областью:

$$ \text{Int}(A \cup B) = A \cup B $$

И здесь снова выполняется включение

$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B). $$

Доказательство

Докажем общее утверждение о том, что объединение внутренностей двух множеств содержится во внутренности их объединения:

$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B). $$

Напомним определение внутренности множества.

Внутренностью множества \( X \) называется множество всех его внутренних точек. Точка \( x \) является внутренней, если существует её окрестность, полностью содержащаяся в \( X \).

Пусть точка \( x \) принадлежит \( \text{Int}(A) \cup \text{Int}(B) \). Тогда она является внутренней либо для множества \( A \), либо для множества \( B \).

• В первом случае существует окрестность \( U_x \), целиком содержащаяся в \( A \).
• Во втором случае существует окрестность \( V_x \), целиком содержащаяся в \( B \).

В любом из этих случаев соответствующая окрестность полностью содержится в объединении \( A \cup B \).

Следовательно, точка \( x \) является внутренней точкой множества \( A \cup B \).

Тем самым показано, что каждая точка множества \( \text{Int}(A) \cup \text{Int}(B) \) принадлежит \( \text{Int}(A \cup B) \), то есть

$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B). $$

Что и требовалось доказать.