집합의 내부

위상공간 \( X \)에서 집합 \( A \)의 내부(interior)는 \( A \) 안에 완전히 포함되는 모든 열린 집합들의 합집합으로 정의된다. 일반적으로 \( \text{Int}(A) \) 또는 \( A^\circ \)라는 기호를 사용한다.

직관적으로 말하면, 집합의 내부는 그 집합 안에서 “가장 넓게 펼쳐질 수 있는 열린 부분”이다.

다시 말해, \( A \) 안에 존재하는 어떤 열린 집합도 \( \text{Int}(A) \)보다 더 클 수는 없다.

Note: 내부는 열린 집합들의 합집합으로 정의되므로, 그 결과 역시 항상 열린 집합이 된다.

보다 엄밀하게 표현하면, 집합 \( A \)의 내부는 \( A \) 안에서 어떤 열린 이웃에 의해 완전히 둘러싸일 수 있는 모든 점들의 집합이다.

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ is open in } X \} $$

즉, 점 \( x \)가 \( \text{Int}(A) \)에 속한다는 것은, \( x \)를 포함하면서 동시에 \( A \) 안에 완전히 들어가는 열린 집합 \( U \)가 적어도 하나 존재한다는 뜻이다.

중요: 집합 \( A \)의 내부는 집합 자체의 성질이 아니라, \( A \)가 포함된 위상공간 \( X \)의 위상 구조에 의해 결정된다. 따라서 같은 집합이라도 어떤 위상을 부여하느냐에 따라 내부는 달라질 수 있다.

구체적인 예

표준 위상이 주어진 실수 공간 \( \mathbb{R} \)에서 집합 \( A = [0, 1] \)을 생각해 보자.

이 집합은 0 이상 1 이하의 모든 실수로 이루어진 닫힌 구간이다.

이 경우 \( A \)의 내부는 열린 구간 \( (0,1) \)이다.

$$ \text{Int}(A) = (0,1) $$

ko interior-of-a-set

이는 0과 1 사이에 있는 점들로 이루어진 가장 큰 열린 구간이다. 경계점인 0과 1은 \( A \) 안에 완전히 포함되는 어떤 열린 구간에도 속하지 않으므로 내부에 포함되지 않는다.

예제 2

이번에는 같은 표준 위상에서 집합 \( A = [0, 1) \)을 살펴보자.

이 집합은 0은 포함하지만 1은 포함하지 않는, 왼쪽은 닫히고 오른쪽은 열린 반열린 구간이다.

이 경우에도 \( A \)의 내부는 앞선 예와 동일하게 \( (0,1) \)이다.

\[ \text{Int}(A) = (0,1) \]

그 이유는 내부가 “집합 안에 완전히 포함되는 모든 열린 집합들의 합집합”으로 정의되기 때문이다.

Note: 표준 위상을 갖는 \( \mathbb{R} \)에서는 열린 구간이 기본적인 열린 집합이다. 따라서 \( [0,1) \) 안에 완전히 포함될 수 있는 최대의 열린 집합은 \( (0,1) \)뿐이다. 왼쪽 끝점 0은 어떤 열린 구간에도 완전히 포함되지 않기 때문에 제외된다.

예제 3

이번에는 집합 \( A = [0,1) \)이 이산 위상이 주어진 위상공간 \( X \) 안에 놓여 있다고 가정하자.

이산 위상에서는 \( X \)의 모든 부분집합이 열린 집합이다.

따라서 \( A \)의 모든 원소는 항상 \( A \) 안에 완전히 포함되는 열린 이웃을 갖는다.

이산 위상이 주어진 \( \mathbb{R} \)에서는 모든 부분집합이 열린 집합이다. 열린 구간, 닫힌 구간, 점들의 임의의 조합까지 모두 열린 집합에 해당한다. 예를 들어 \( (0,0.5) \), \( (0.25,0.75) \), \( (0,1) \)뿐 아니라, \( A=[0,1) \)에 포함된 \( [0,0.25] \), 공집합, 그리고 \( [0,1) \) 자체도 열린 집합이다.

따라서 이 위상에서는 \( A = [0,1) \) 자체가 열린 집합이 된다.

그 결과, 이 경우 집합 \( A \)의 내부는 \( A \) 자신과 정확히 일치한다.

$$ \text{Int}(A) = A = [0,1) $$

이산 위상에서는 어떤 집합이든 그 내부가 항상 집합 자체와 같다.https://www.ecoage.org/ko/math/ko-how-to-determine-the-interior-of-a-set-in-r

Note: 이 예는 위상의 선택이 집합의 내부와 이웃의 개념에 얼마나 큰 영향을 미치는지를 잘 보여준다. 이러한 성질은 집합 \( A \) 자체가 아니라, 그것이 정의된 위상공간 \( X \)의 구조에 의해 결정된다.

예제 4

점들의 집합 \( \{a, b, c\} \)로 이루어진 위상공간 \( X \)에 이산 위상을 부여해 보자.

이 경우 정의에 따라 \( X \)의 모든 부분집합은 열린 집합이다.

• \( \emptyset \)와 \( \{a, b, c\} \)는 열린 집합이다.
• 각 점 \( \{a\} \), \( \{b\} \), \( \{c\} \) 역시/ko/math/ko-the-union-of-interiors-of-two-sets 열린 집합이다.
• \( \{a, b\} \), \( \{a, c\} \), \( \{b, c\} \)와 같은 부분집합도 모두 열린 집합에 해당한다.

이제 부분집합 \( A = \{b, c\} \subseteq X \)를 살펴보자.

내부의 정의에 따라 \( \text{Int}(A) \)는 \( A \) 안에 포함되는 모든 열린 집합들의 합집합이다.

\( A \)에 포함되는 열린 집합은 \( \{b\} \), \( \{c\} \), 그리고 \( \{b, c\} \)이다.

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

따라서 이들의 합집합은 정확히 \( A \)와 일치한다.

결론적으로 \( \text{Int}(A) = A \)가 성립한다.

Note: 이 결과는 특정 집합에만 적용되는 것이 아니다. 이산 위상공간에서는 모든 부분집합이 열린 집합이므로, 임의의 부분집합 \( S \subseteq X \)에 대해 항상 \( \text{Int}(S) = S \)가 성립한다.

집합의 내부 정리

위상공간 \( X \)에서 부분집합 \( S \subseteq X \)와 점 \( y \in X \)에 대해, 점 \( y \)가 집합 \( S \)의 내부에 속한다는 것은 \( \text{Int}(S) \)로 표기하며, 이는 \( y \)를 포함하면서 동시에 \( S \) 안에 완전히 포함되는 열린 집합 \( U \)가 존재할 때 그리고 그때에만 성립한다. 이를 수식으로 나타내면 다음과 같다. $$ y \in \text{Int}(S) \iff \exists \ U \text{ (열린 집합)}, \ y \in U \subseteq S $$

직관적으로 말하면, 점 \( y \)가 집합 \( S \)의 내부에 속한다는 것은 \( y \)가 집합 \( S \) 안쪽에 “여유를 두고” 들어 있는 열린 영역에 포함되어 있다는 뜻이다.

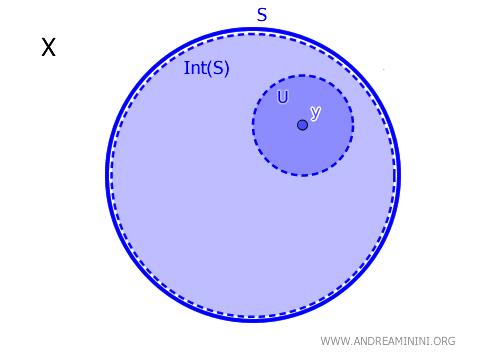
이 정리는 위상공간 \( X \)에서 한 점이 집합의 내부에 속하는지를 판단할 수 있는 간결하면서도 강력한 필요충분조건을 제공한다.

증명

• 필요조건: \( y \in \text{Int}(S) \)라고 하자. 내부의 정의에 따라, \( X \)에는 열린 집합 \( U \)가 존재하여 \( y \in U \)이고 동시에 \( U \subseteq S \)를 만족한다. 따라서 이러한 열린 집합 \( U \)의 존재는 반드시 필요하다.
• 충분조건: 반대로, \( y \in U \subseteq S \)를 만족하는 열린 집합 \( U \)가 존재한다고 가정하자. 내부는 \( S \) 안에 포함되는 모든 열린 집합들의 합집합으로 정의되므로, \( U \)에 속한 모든 점은 \( \text{Int}(S) \)에 포함된다. 특히 \( y \) 역시 \( \text{Int}(S) \)에 속하게 된다.

Note: 이 정리는 열린 집합이라는 개념을 “집합 안에 속한다”는 조건과 직접적으로 연결해 준다. 이러한 연결은 연속성, 극한, 경계 개념 등 다양한 위상적 성질을 이해하는 데 핵심적인 역할을 한다.

예제

표준 위상이 주어진 실수 공간 \( \mathbb{R} \)에서 집합 \( A = [1,3] \)을 고려해 보자.

$$ A = [1,3] $$

이 집합은 1 이상 3 이하의 모든 실수로 이루어진 닫힌 구간이다.

이제 집합의 내부 정리를 이용하여 \( A \)의 내부를 구해 보자.

\( A \)의 내부를 찾기 위해서는, \( A \) 안에 완전히 포함되는 열린 집합 \( U \)를 찾으면 된다. 그러한 \( U \)에 속하는 점들은 모두 \( \text{Int}(A) \)에 포함된다.

1. \( U \)의 선택
   열린 구간 \( U = (1,3) \)을 선택한다. 이는 실수 공간 \( \mathbb{R} \)의 표준 위상에서 열린 집합이다.
2. \( U \subseteq A \) 확인
   열린 구간 \( (1,3) \)의 모든 점은 닫힌 구간 \( [1,3] \)에 포함된다. 단, 끝점 1과 3은 열린 구간에 포함되지 않는다.

따라서 \( U = (1,3) \)은 집합 \( A \) 안에 완전히 포함되는 열린 집합이며, 이로부터 집합 \( A \)의 내부는 정확히 \( (1,3) \)임을 알 수 있다.

Note: 이 예제에서 볼 수 있듯이, 경계점 1과 3은 이 점들을 포함하면서 동시에 \( A \) 안에 완전히 들어가는 열린 집합이 존재하지 않으므로 \( \text{Int}(A) \)에 포함되지 않는다.

내부의 기본 성질

이제 집합의 내부와 관련된 몇 가지 중요한 성질들을 살펴보자. 이 성질들은 내부, 폐포, 합집합, 교집합과 같은 위상적 연산들 사이의 관계를 명확하게 드러낸다.

• 내부의 합집합에 대한 포함 관계
  두 집합의 내부의 합집합은 항상 그 합집합의 내부에 포함된다. $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
• 내부와 교집합의 관계
  두 집합의 내부의 교집합은 그 교집합의 내부와 정확히 일치한다. $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
• 여집합의 내부와 폐포의 여집합
  집합 \( A \)의 여집합의 내부는 \( A \)의 폐포의 여집합과 같다. $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
• 여집합의 폐포와 내부의 여집합
  집합 \( A \)의 여집합의 폐포는 \( A \)의 내부의 여집합과 같다. $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

추가 참고 사항

아래는 집합의 내부를 이해하는 데 도움이 되는 몇 가지 보조 성질과 설명이다.

• \( U \)가 열린 집합이고 \( U \subseteq A \)이면, \( U \subseteq \text{Int}(A) \)
  열린 집합 \( U \)가 집합 \( A \) 안에 완전히 포함되어 있다면, 정의에 따라 \( U \)는 \( A \)의 내부에 포함된다. 내부는 \( A \) 안에 포함되는 가장 큰 열린 집합이기 때문이다.
• \( A \subseteq B \)이면, \( \text{Int}(A) \subseteq \text{Int}(B) \)
  집합 사이의 포함 관계는 내부 연산에 의해서도 유지된다.
• 집합 \( A \)가 열린 집합일 필요충분조건은 \( A = \text{Int}(A) \)
  집합 \( A \)가 열린 집합이라는 것은, 모든 점이 \( A \) 안에 완전히 포함되는 열린 이웃을 갖는다는 것과 동치이며, 이는 곧 \( A = \text{Int}(A) \)임을 의미한다.
• R 언어를 이용한 내부 계산
  R은 수학적·통계적 계산에 적합한 언어로, 위상적 개념을 실험적으로 탐구하거나 내부를 계산하는 데에도 활용할 수 있다.

이러한 성질들은 위상수학 전반에서 반복적으로 사용되며, 보다 복잡한 개념을 이해하기 위한 중요한 기초를 이룬다.