열린 공

위상수학에서 open ball, 즉 열린 공은 중심점 c로부터 거리 r보다 가까운 모든 점들의 집합을 뜻한다. 열린 원반이나 열린 구로도 불리며, 다음과 같은 형태로 정의된다. $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

이 개념은 계량함수 \( d \)가 주어진 계량공간 \( M \)에서 사용되며, \( d \)는 두 점 사이의 거리를 재는 역할을 한다. 이러한 구조는 공간의 형태를 이해하는 데 매우 중요하다.

열린 공은 중심과 반지름이라는 단순한 두 요소로 결정되기 때문에 직관적으로 접근하기 쉽다.

위상수학에서 열린 집합이라는 성질은 특히 중요한데, 열린 공의 특징도 여기에 기반한다. 열린 공 안의 임의의 점을 잡으면, 그 점을 중심으로 한 더 작은 열린 공을 항상 만들 수 있으며, 이 작은 열린 공은 원래의 열린 공 속에 완전히 포함된다.

Note: 열린 공은 크기를 바꾸거나 위치를 옮겨도 그 본질이 변하지 않는다. 이러한 변환에도 불구하고 열린 공의 위상적 성질은 그대로 유지된다.

R² 평면에서 이를 살펴보면 이해가 한층 더 쉬워진다. 점 p=(x,y)와 중심 c=(x₀,y₀) 사이의 거리는 유클리드 계량으로 정의된다.

$$ d(p,c) = \sqrt{(x-x_0)^2 + (y-y_0)^2} $$

이렇게 정의된 열린 원반은 R²의 위상을 구성하는 기본 단위이며, 평면의 공간 구조를 설명하는 핵심적인 도구다.

R²의 표준 위상은 바로 이러한 열린 공들의 집합을 바탕으로 만들어진다.

$$ B = \{ B(p, r) \ | \ p \in R^2, \ r > 0 \} $$

여기서 p는 R²의 한 점, r은 열린 공의 반지름이다.

물론 R²에는 여러 가지 위상을 정의할 수 있지만, 가장 널리 쓰이고 기본적인 구조는 이 표준 위상이다.

열린 공의 중요한 성질 하나는 모든 점 \( q \in B(p,r) \)에 대해, 그 점을 중심으로 하는 더 작은 열린 공 B(q, ε)이 존재하며, 이 열린 공이 B(p,r) 안에 완전히 포함된다는 점이다.

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ such \ that \ B(q,\epsilon;) \subset B(p,r) $$

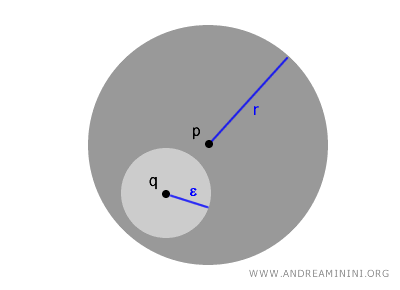
이 구조적 특징은 다양한 공간에서 반복적으로 나타나며, 위상수학의 기본 개념을 이해하는 데 중요한 기반이 된다.