위상수학에서의 연결성 이해하기

위상수학에서 어떤 공간이 서로 떨어진 열린집합들의 합으로 나뉘지 않는다면, 그 공간은 연결되어 있다고 말합니다. 쉽게 말해, 연결성은 공간 안의 임의의 두 점을 공간을 벗어나지 않고 하나의 경로로 이어줄 수 있는 성질입니다.

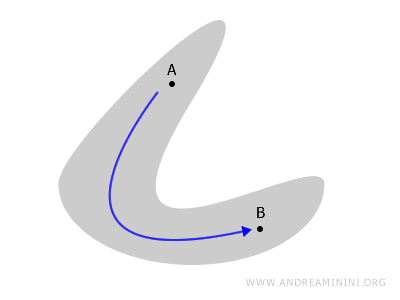
연결성은 공간의 부분들이 얼마나 자연스럽게 이어져 있는지를 보여주는 개념으로, 위상수학에서 연속성과 더불어 가장 기본적이고 중요한 주제입니다.

이는 열린 집합을 통해 정의되기 때문에 위상적 성질이다.

이 개념은 단순히 이론적인 것에 그치지 않고, 공간의 구조를 이해하고 분류하는 데 결정적인 역할을 합니다. 수학의 다양한 분야에서 ‘공간이 어떻게 연결되어 있는가’를 이해하는 것은 그 자체로 큰 통찰을 제공합니다.

직관적인 예시로 살펴보기

평면 도형이나 다면체를 떠올려 봅시다. 공간 내부의 두 점 A와 B를 공간을 벗어나지 않고 하나의 연속적인 경로로 연결할 수 있다면, 그 공간은 연결공간입니다.

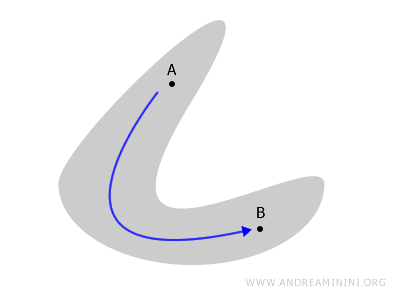
하지만 공간이 여러 조각으로 떨어져 있다면, 그 공간은 더 이상 하나의 연결된 전체로 볼 수 없습니다. 이런 공간을 비연결공간이라고 부릅니다.

예를 들어 아래 그림처럼, 두 영역이 완전히 분리되어 있을 경우 A와 B를 연결하는 모든 경로는 공간 밖으로 벗어나야 합니다.

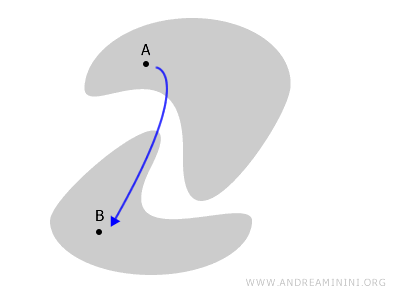
비연결공간의 간단한 비유

두 개의 방이 벽으로 나누어진 건물을 떠올려 봅시다. 이 두 방은 벽(경계)을 포함하지 않는 서로 다른 열린집합으로, 서로 완전히 분리되어 있습니다.

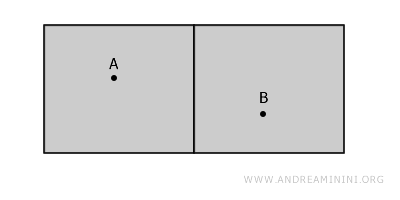
겉으로 보기에는 두 방이 같은 건물 안에 있으니 연결된 것처럼 보이지만, 실제로는 그렇지 않습니다. A에서 B로 이동하려면 벽을 통과해야 하는데, 벽은 우리가 정의한 공간의 일부가 아니기 때문입니다.

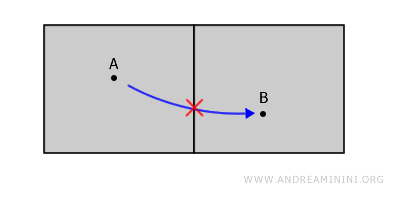
이 예시를 통해 알 수 있듯이, 열린집합의 경계는 그 집합에 포함되지 않습니다. 이것이 연결성의 핵심적인 아이디어입니다.

국소적 연결성: 작은 영역 안에서의 연결

국소적 연결성이란, 공간의 각 점이 자신을 포함하는 연결된 열린 근방(neighborhood)을 가진다는 뜻입니다. 즉, 공간 전체는 분리되어 있어도, 작은 부분에서는 연결되어 있을 수 있다는 개념입니다.

앞서의 예시처럼, 두 개의 분리된 방으로 구성된 공간을 생각해봅시다.

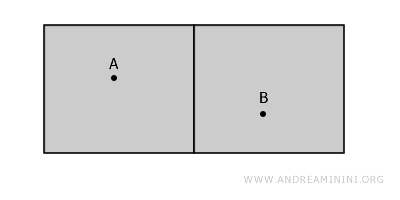
이 공간 전체는 벽을 통과하지 않고는 A와 B를 연결할 수 없기 때문에 비연결공간이지만, 점 A 주변에는 A를 포함하면서 내부의 모든 점이 서로 연결된 영역이 존재합니다. 이것이 바로 국소적 연결성의 사례입니다.

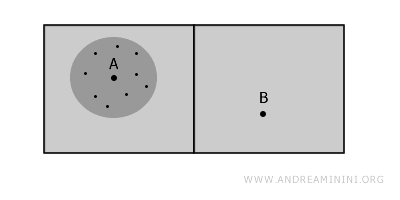
마찬가지로 점 B 역시 자신이 속한 영역 안에서는 국소적으로 연결되어 있습니다.

연결성의 두 가지 대표 형태

연결성에도 여러 형태가 있지만, 기본적으로 많이 다루는 두 가지는 경로 연결성과 단일 연결성입니다.

• 위상적 연결성 (Topological Connectedness)
  위상 공간 $ X $가 연결(connected)되었다는 것은, 그 공간을 두 개의 공집합이 아닌 서로소(open, disjoint) 열린 집합으로 분리할 수 없다는 뜻이다. 다시 말해, 공간을 완전히 나누는 독립된 두 영역이 존재하지 않는다는 의미이다.

  예시. 구간 (-1, 1)은 연결되어 있지만, (-1, 0) ∪ (0, 1)은 그렇지 않다. 왜냐하면 두 개의 서로소이면서 공집합이 아닌 열린 집합 (-1, 0)과 (0, 1)이 존재하며, 이 둘을 합치면 전체 공간을 덮을 수 있기 때문이다.
  따라서 이 두 집합은 공간의 분리(separation)를 이룬다.

• 경로 연결성 (Path Connectedness, 또는 Arc Connectedness)
  위상 공간이 경로 연결(path connected)되어 있다는 것은, 공간 안의 임의의 두 점 A와 B를 잇는 연속적인 경로가 존재하며, 그 경로가 전부 그 공간 내부에 포함되어 있음을 뜻한다. 모든 경로 연결 공간은 연결 공간이지만, 그 역은 반드시 성립하지 않는다.

  예를 들어 평면 위의 닫힌 도형을 떠올려 보자. 도형 내부의 임의의 두 점 A와 B 사이에는 펜을 종이에서 떼지 않고 도형 밖으로 벗어나지 않으면서 그릴 수 있는 연속적인 곡선이 존재한다.
  
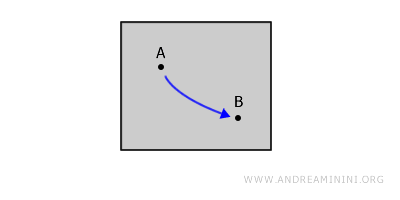
  호 연결성과 경로 연결성의 차이.  두 개념은 비슷하지만, 호 연결성(arc connectedness)에서는 경로가 일대일이어야 한다. 즉, 경로가 자기 자신과 교차하거나 동일한 점을 두 번 지나면 안 된다.

• 단일 연결성 (Simple Connectivity)
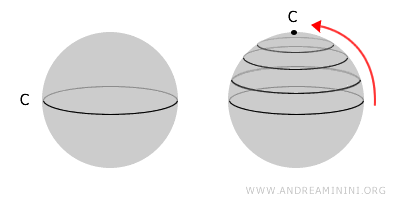
  공간 안의 모든 닫힌 곡선이 하나의 점으로 수축될 수 있다면, 그 공간은 단일연결공간이라고 부릅니다. 이는 공간 내부에 구멍이 없다는 뜻입니다. 단일연결공간은 항상 연결공간이지만, 모든 연결공간이 단일연결인 것은 아닙니다.

  예를 들어, 구(sphere)는 표면 위의 어떤 닫힌 곡선도 한 점으로 수축할 수 있기 때문에 단일연결공간입니다. 반면 도넛 모양의 고리(torus)는 중심에 구멍이 있기 때문에 모든 곡선을 한 점으로 줄일 수는 없습니다. 즉, 연결되어 있긴 하지만 단일연결은 아닙니다.
  
  
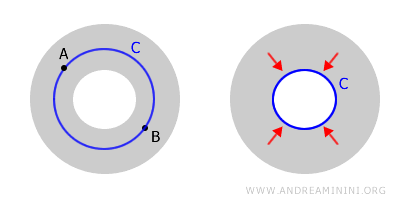
  이런 공간은 다중연결공간이라 부르며, 고리 모양의 환상공간이 대표적인 예입니다.

마무리하며

연결성은 단순히 공간이 “하나로 이어져 있는가”를 넘어, 그 내부 구조와 관계를 드러내는 개념입니다. 수학적 사고뿐만 아니라 현실 세계의 연속성과 구조를 이해하는 데에도 중요한 단서가 됩니다.

• 참고로, 실수의 집합에서 연결된 공간은 오직 하나의 구간(interval)뿐입니다.