열린집합과 위상 이해하기

정리하면, T는 열린집합만을 포함해야 하며, 열린집합끼리 합치거나 교차했을 때 다시 열린집합이 되어야 한다. 이렇게 함으로써 열린집합의 성질이 위상 안에서 안정적으로 유지된다.

여기서 집합족이란, 원소가 집합으로 이루어진 집합을 의미한다.

이와 같은 조건을 만족하면, 집합 X와 위상 T는 함께 하나의 위상공간을 이룬다. 이는 보통 (X, T)라고 표기한다.

Note. 간단히 X를 위상공간이라 부르기도 하지만, 실제로 위상공간은 X 자체와 그 위에서 정의된 위상 T라는 두 요소를 모두 포함한다는 점을 잊지 말아야 한다.

공집합은 왜 열린집합인가

공집합이 열린집합으로 인정되는 이유는 위상을 구성하는 공리가 논리적 충돌 없이 유지되도록 하기 위한 것이다. 이 규칙을 포함해야 위상 전체가 일관되고 완전한 구조를 갖는다.

예제로 살펴보는 위상

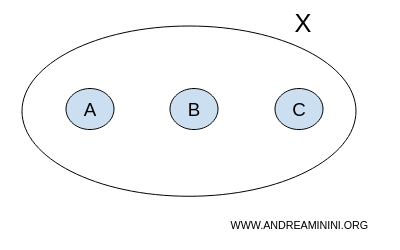
이제 세 원소 A, B, C로 이루어진 집합 X를 생각해 보자.

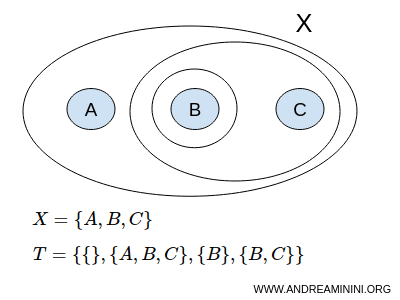
$$ X = \{ A,B,C \} $$

다음과 같은 집합족 T를 위상으로 선택한다고 해 보자.

$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \}  \} $$

여기서 { }는 공집합 Ø를, {A,B,C}는 전체집합 X를 의미한다. 정의에 따르면 이 둘은 무조건 열린집합이다.

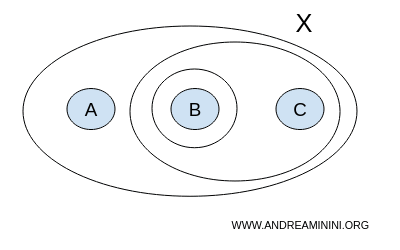
이제 열린집합의 조건을 직접 확인해보자. 먼저 위상 T 안에서 가능한 합집합을 계산하면 결과가 모두 다시 T 안에 포함된다.

$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$ $$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$ $$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$ $$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$

따라서 T는 합집합 연산에 대해 닫혀 있는 집합족이다. 다음으로 교집합의 경우도 살펴보자.

$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$ $$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$ $$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$ $$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$

교집합 역시 항상 T 안에 머무르므로, T는 교집합 연산에 대해서도 닫혀 있다. 따라서 이 T는 X 위의 위상이 된다.

위상이 아닌 경우

이번에는 앞선 예와 비슷하지만 한 가지 다른 집합족 T를 생각해 보자.

$$ X = \{ A,B,C \} $$

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

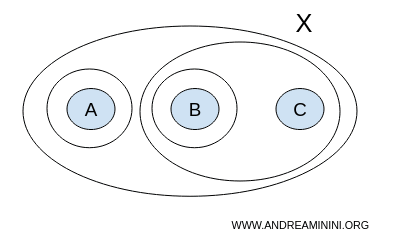
이 경우에는 열린집합의 조건을 위반한다. 예를 들어 {A}와 {B}는 T 안에 있으므로 열린집합이지만, 두 집합의 합집합 {A,B}는 T에 포함되지 않는다.

$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T  $$

열린집합들의 합집합이 열린집합을 보장하지 못하므로, 이 집합족은 더 이상 위상이 될 수 없다.

즉, 모든 조건을 만족해야만 하나의 위상을 정의할 수 있다. 이러한 과정을 통해 어떤 집합족이 위상이 될 수 있는지 판단하게 된다.