닫힌집합
위상공간 X의 부분집합 B가 닫힌집합이 되기 위한 필요충분조건은 다음과 같다. 여집합 X-B에 속하는 임의의 점 u∈X-B에 대해, u를 포함하면서도 여전히 여집합 X-B 안에 완전히 들어가는 근방이 존재해야 한다.
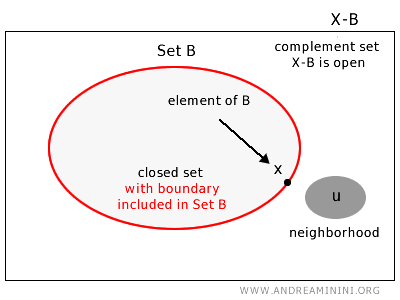
닫힌집합이란 집합의 경계를 모두 포함하는 집합을 의미한다.
보다 엄밀하게 말하면, 위상공간 X의 부분집합 B가 닫힌집합이라는 것은 여집합 X-B가 열린집합일 때 성립한다.
참고: 이 정의는 닫힌집합 B에는, 그 점을 중심으로 한 근방이 B 전체 안에 완전히 포함되지 않는 경계점이 존재할 수 있음을 내포한다.
직관적 예시
실수 전체의 집합 R에서 닫힌구간을 생각해 보자.
닫힌구간이란? 실수 a와 b에 대해 $ a \lt b $일 때, 조건 a≤x≤b를 만족하는 모든 실수 x의 집합을 닫힌구간이라 한다.
닫힌구간은 [a,b]로 표기하며, 대괄호는 구간의 양 끝점 a와 b가 집합에 포함되어 있음을 나타낸다.
예를 들어 [3,10]은 실수직선 R에서 대표적인 닫힌집합이다.
이 경우 닫힌구간 B는 3과 10을 포함해, 그 사이의 모든 실수로 이루어진다.
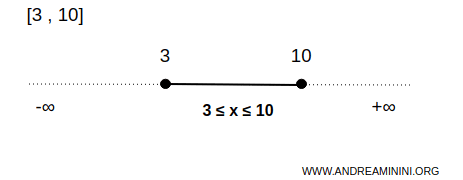
즉, 3≤x≤10을 만족하는 모든 점이 포함되며 끝점 역시 예외가 아니다.
다만 구간 전체의 각 점이 자신을 중심으로 한 근방을 온전히 [3,10] 내부에 둘 수 있는 것은 아니다.
예를 들어 x=3의 임의의 근방은 일부가 구간 밖으로 나가기 때문에 [3,10]에 완전히 포함되지 않는다.
참고: 예를 들어 3±0.00000001과 같은 극도로 작은 근방을 고려하더라도 3-0.00000001은 3보다 작으므로 구간 밖으로 벗어난다. x=10에서도 동일한 현상이 발생한다.
이 예시는 1차원 공간에서 닫힌집합의 본질을 명확하게 보여준다.
또 다른 닫힌집합의 예
이번에는 2차원 평면에서 닫힌집합을 살펴보자. 중심이 (0,0)이고 반지름이 r=1인 원을 생각하면, 다음과 같은 집합을 얻을 수 있다.
$$ x^2+y^2≤1 $$
이 부등식은 중심에서의 거리가 1 이하인 모든 점을 포함하며, 원 내부와 원 위의 점을 모두 포함한다.
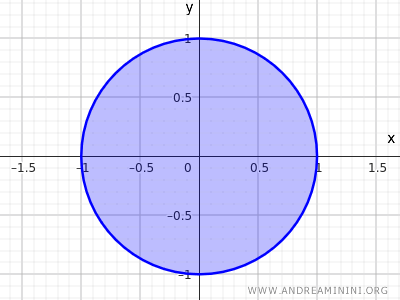
이는 닫힌집합의 대표적인 2차원 예다.
직관적으로, 원의 경계 위에 있는 점들은 자신을 중심으로 한 임의의 근방이 원 안에 온전히 머물 수 없다는 특징을 가진다.
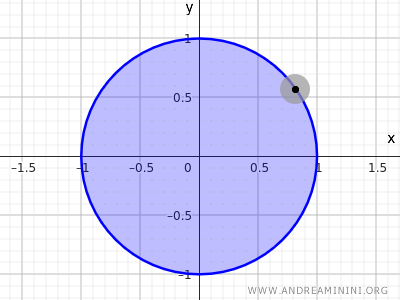
참고: 방정식 $ x^2+y^2=1 $로 표현되는 원은 경계만을 포함하여 내부를 배제하므로 R2의 표준위상에서 열린집합도 닫힌집합도 아니다. 반면 $ x^2+y^2≤1 $과 같이 경계와 내부를 모두 포함하는 경우는 경계점을 모두 포함하므로 닫힌집합이 된다.
이 개념은 3차원에서는 구로, 더 나아가 n차원에서는 n차원 구체로 확장된다.
닫힌집합과 여집합
공간 X에서 닫힌집합 C의 여집합 X-C는 열린집합이다.
C가 닫힌집합이라면 여집합 X-C는 필연적으로 열린집합이 된다.
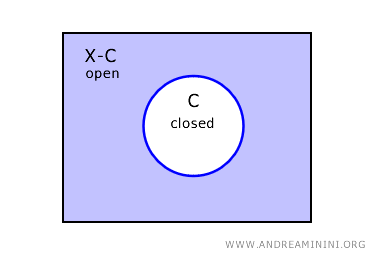
반대로 어떤 집합 U가 열린집합이라면 그 여집합 X-U는 닫힌집합이 된다.
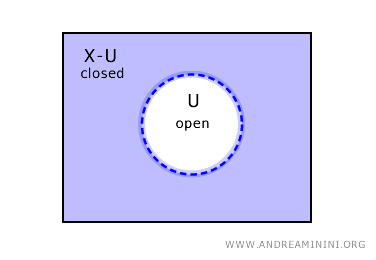
그러나 이것이 전부는 아니다. 위상공간에서는 열리면서 닫힌집합(폐열집합)도 존재하며, 열리지도 닫히지도 않은 집합도 존재할 수 있다.
따라서 닫히지 않았다는 이유만으로 자동적으로 열린집합이라 할 수 없으며, 열리지 않았다고 해서 곧바로 닫힌집합이라 할 수도 없다.
예시
집합 X={a,b,c,d}에 위상 T가 주어져 있다고 하자.
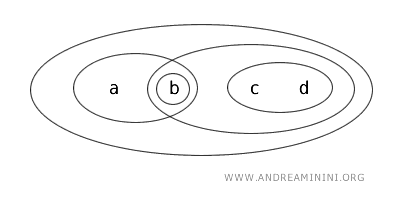
이 위상에서 열린집합으로 분류되는 것은 {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, ∅ 이다.
이를 항목별로 살펴보면 다음과 같다.
- {b}는 열린집합이다. 위상 T에서 열린집합으로 명시되어 있기 때문이다.
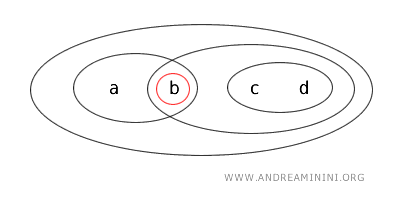
- {a}는 닫힌집합이다. 여집합 X-{b,c,d}가 {a}가 되며, 이 여집합이 열린집합이기 때문이다.
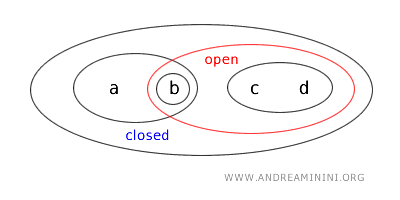
- {a,b}는 열리면서 닫힌집합(폐열집합)이다. 일반적인 위상공간에서 충분히 나타날 수 있는 형태로, {a,b}는 열린집합으로 지정되어 있으며 그 여집합 또한 열린집합이므로 닫힌집합이기도 하다.
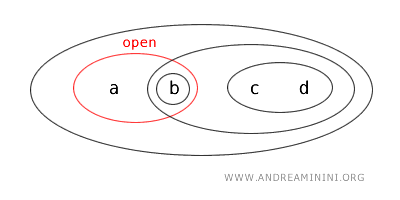
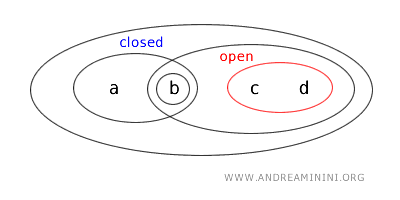
- {b,c}는 열린집합도 닫힌집합도 아니다. 열린집합 조건을 만족하지 않으며, 여집합 역시 열린집합이 아니기 때문이다.
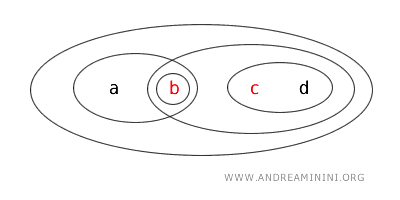
이 예시는 하나의 위상에서 어떤 집합은 열릴 수도 있고, 닫힐 수도 있으며, 두 성질을 동시에 가질 수도 있고, 어느 쪽에도 속하지 않을 수도 있음을 명확히 보여준다.
닫힌집합의 성질
닫힌집합은 열린집합의 여집합으로 정의되며, 다음과 같은 핵심적 성질을 지닌다.
- 공집합(Ø)과 전체공간 X는 항상 닫힌집합이다.
- 임의 개수의 닫힌집합에 대한 교집합은 다시 닫힌집합이다.
- 유한 개수의 닫힌집합에 대한 합집합 역시 닫힌집합이다.
예시
유클리드 공간 Rn의 표준위상에서는 한 점으로 이루어진 집합은 항상 닫힌집합이다.
예를 들어 실수직선 R1에서 한 점 n을 생각하면, {n}의 여집합은 실수 전체에서 n을 제외한 모든 점으로 이루어진 집합이다.
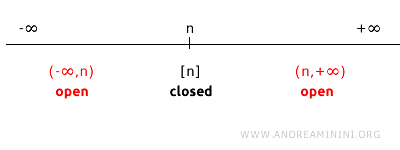
이 여집합은 두 열린구간 (-∞, n)과 (n, +∞)의 합집합으로 표현된다.
표준위상에서 두 구간 (-∞, n)과 (n, +∞)는 열린집합이며, 열린집합의 합집합도 열린집합이므로, {n}의 여집합은 열린집합이 된다.
따라서 {n}은 닫힌집합임을 알 수 있다.
그러나 한 점이 언제나 닫힌집합이 되는 것은 아니다. 이러한 성질은 공간에 부여된 위상에 따라 달라진다.
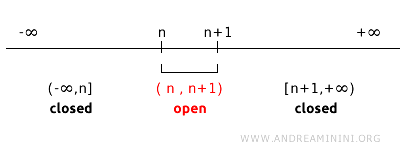
정수 n에 대해 (n, n+1) 형태의 열린구간들로 생성된 위상을 생각해 보자. 이 위상에서는 한 점 n을 포함하는 적절한 열린근방이 존재하지 않으므로, {n}은 닫힌집합이 아니다. 예를 들어 열린집합 (1,2)의 여집합은 (-∞, 1] ∪ [2, +∞)이며, (2,3)의 여집합은 (-∞, 2] ∪ [3, +∞)가 된다. 이 위상에서는 한 점을 여집합 형태로 얻을 수 없으므로 {n}은 닫힌집합이 아니다. 즉 닫힌집합의 성질은 위상 선택에 의해 결정된다.
각주
다음은 닫힌집합과 관련된 보충 관찰들이다.
- 닫힌집합과 극한점
어떤 점이 극한점이라는 것은, 그 점을 중심으로 하는 임의의 근방 안에 항상 집합의 다른 점이 존재함을 의미한다. 닫힌집합은 모든 극한점을 포함하는 집합이며, 반대로 열린집합은 극한점을 모두 포함하지 않을 수도 있다.예시: 닫힌구간 [0,1]을 생각해 보자. 이 구간의 임의의 점, 예를 들어 내부점 0.5는 어떤 근방을 잡더라도 [0,1] 안의 다른 점들을 무수히 포함하므로 극한점이다.
![닫힌구간 [0,1]에서의 0.5 극한점 예시](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-1.gif)
경계점에서도 동일한 현상이 나타난다. 예를 들어 0 근방의 점 0.1, 0.01, 0.001 등은 모두 [0,1] 안에 존재하므로 0 역시 극한점이다.
![[0,1] 경계의 극한점 예시](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-2.gif)
이처럼 닫힌구간 [0,1]의 모든 점은 극한점의 성질을 지닌다. - 닫힌집합의 정의적 성질: A는 닫힌집합 ⇔ A = Cl(A)
위상공간에서 집합 \( A \)가 닫힌집합이라는 것은, 그 집합이 닫힘과 일치함을 의미한다. 즉 \( A = \text{Cl}(A) \)일 때, A는 닫힌집합이다. 닫힘 Cl(A)는 A와 그 극한점을 모두 포함하므로, 극한점을 빠짐없이 포함하는 집합은 닫힌집합이 된다.
등등.