위상수학

위상수학은 물체가 찢어지거나 서로 접합되지 않는 한, 늘이기, 굽히기, 비틀기와 같은 연속적 변형 아래에서도 변하지 않는 공간의 성질을 연구하는 수학의 한 분야이다.

핵심은 변환이 연속적인 동안 유지되는 기하학적 성질을 이해하는 데 있다.

이러한 성질은 공간의 일부를 찢거나 서로 다른 부분을 붙이는 것처럼 연속성이 깨지는 조작을 통해서만 변화한다.

예를 들어, 구와 정육면체는 위상적으로 동형이다. 이는 어떠한 찢김이나 접합도 없이 하나를 다른 하나로 연속적으로 변형할 수 있기 때문이다.

반면, 구와 토러스는 위상적으로 동형이 아니다. 한쪽을 다른 쪽으로 바꾸려면 구멍을 생성하거나 제거해야 하며, 이는 필연적으로 찢기거나 붙이는 과정을 수반한다.

다시 말해, 위상수학은 거리, 크기, 모양과 같은 정밀한 계량적 특성보다 공간이 어떻게 배열되고 서로 연결되어 있는지를 중점적으로 다룬다.

위상적 관점에서는 길이, 면적, 부피, 각도와 같은 개념은 본질적인 의미를 갖지 않는다. 대신 중요한 것은 도형의 질적 성질과, 연속적 변형을 통해 서로 변환 가능한지의 여부이다.

이러한 관점에는 예를 들어 연결성, 콤팩트성, 대상이 지니는 구멍의 개수, 그리고 공간의 다양한 전역적 성질들이 포함된다.

위상수학은 위상공간이라는 기본 개념을 도입하며, 그 중심에는 위상동형사상이 있다. 이는 공간의 위상적 구조를 보존하면서 공간을 연속적으로 변형하는 가역적인 사상이다.

이러한 이유로 위상수학은 흔히 “고무판 기하학”으로 비유된다. 즉, 대상은 탄성 물질로 이루어져 있어 늘리거나, 굽히거나, 압축할 수는 있지만, 찢거나 붙일 수는 없다고 상상한다. 위상수학은 현대 수학에서 핵심적인 역할을 하며, 다양한 분야를 하나의 관점으로 연결하는 강력한 이론적 틀을 제공한다.

위상수학의 탄생

위상수학의 시작은 18세기로 거슬러 올라갑니다. 수학자 레온하르트 오일러(Leonhard Euler)는 쾨니히스베르크의 일곱 다리 문제를 통해 새로운 사고의 문을 열었습니다.

그는 다음과 같은 질문을 던졌습니다: "강 위에 있는 일곱 개의 다리를 모두 한 번씩만 건너는 길이 존재할까?" - 이 단순한 퍼즐은 거리나 길이와는 전혀 관계가 없는, 순수한 연결성의 문제였습니다.

쾨니히스베르크의 일곱 다리 문제

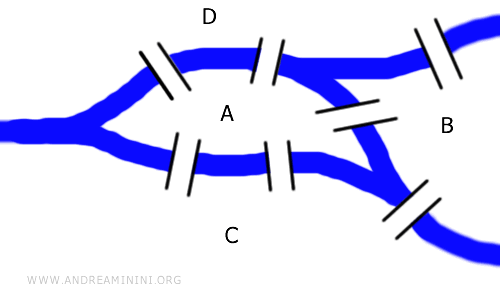
오일러는 이 문제를 그래프로 표현했습니다. 정점은 땅이나 섬, 선은 다리를 나타내죠. 아래의 그래프는 원래 도시의 구조와 위상적으로 동일한 형태입니다.

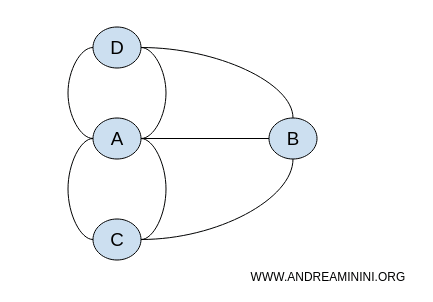
정점이 정확히 어디에 있느냐는 중요하지 않습니다. 중요한 것은 무엇이 무엇과 연결되어 있는가입니다.

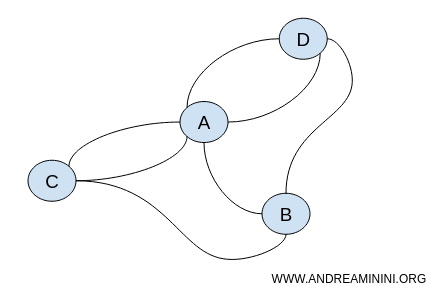
이 단순한 그래프 사고가 바로 위상수학의 출발점이 되었습니다.

오일러는 이 문제가 거리의 계산이 아닌 공간의 관계성에 관한 것임을 보여주었고, 결국 이 문제는 "위치의 기하학(geometry of position)"이라는 새로운 수학 개념을 탄생시켰습니다.

위상수학의 발전

19세기에는 가우스, 뫼비우스, 리스팅, 리만, 클라인 같은 위대한 수학자들이 곡면과 형태의 성질을 연구하며 위상적 사고를 발전시켰습니다.

Trivia: '위상학(Topology)'이라는 용어는 요한 리스팅(Johann Listing)이 1847년에 처음 사용했습니다. 그러나 학계에서 널리 자리 잡기까지는 수십 년이 걸렸습니다.

이후 푸앵카레(Poincaré)는 대수적 위상수학을 세우며 위상적 사고를 더욱 심화시켰고, 20세기에는 하우스도르프, 칸토어, 브라우어 등 여러 학자들이 이 분야를 수학의 중심으로 끌어올렸습니다.

오늘날 위상수학은 기하학과 해석학을 잇는 다리 역할을 하며, 수학뿐 아니라 물리학, 경제학, 데이터 과학 등에도 깊이 응용되고 있습니다.

위상공간의 개념

위상수학의 기본 단위는 위상공간입니다. 위상공간은 간단히 말해, 집합 \( X \)에 위상이라 불리는 구조 \( T \)를 부여한 형태로, 연속성이나 근접성, 극한을 일반화하여 다룰 수 있는 틀입니다.

$$ (X,T) $$

예시: 실수 직선 \( \mathbb{R} \)은 대표적인 위상공간입니다. 이때 열린 구간을 포함하는 집합을 '열린집합'이라 부르며, 이를 통해 연속성이나 극한 개념을 탐구할 수 있습니다.

커피잔과 도넛의 관계

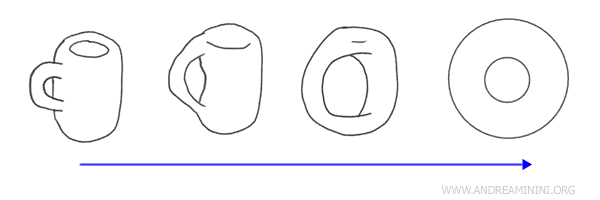
위상수학의 가장 유명한 예시 중 하나는 바로 커피잔과 도넛입니다. 얼핏 보면 전혀 다른 모양 같지만, 사실 두 도형은 위상적으로 동일합니다. 둘 다 구멍이 하나 있기 때문입니다.

준동형사상(Homeomorphism): 위상수학에서는 자르거나 붙이지 않고, 연속적으로 변형하여 한 공간을 다른 공간으로 바꿀 수 있다면, 두 공간은 '같은' 것으로 봅니다.

기하학 vs 위상수학

기하학과 위상수학은 모두 공간을 다루지만, 시선이 다릅니다.

• 기하학은 거리, 각도, 길이처럼 정량적인 성질을 연구합니다. 도형의 회전, 대칭, 이동 등이 여기에 해당하죠.
  

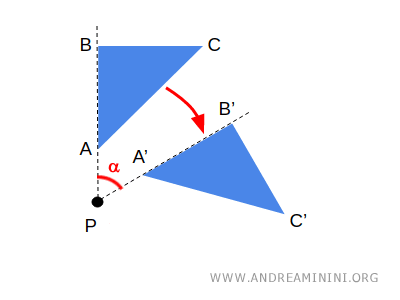
  유클리드 기하학이 대표적이지만, 비유클리드 기하학은 평행선 공리를 수정하거나 배제하면서 더 넓은 공간의 세계를 탐구합니다.

• 위상수학은 거리를 무시하고 형태의 연결성에 주목합니다. 잘라내거나 붙이지 않고 단지 늘리거나 구부려서 얻을 수 있는 변형이라면, 그것은 본질적으로 같은 형태로 봅니다.
  

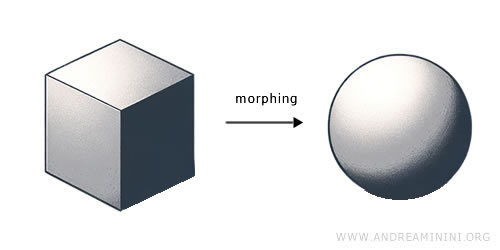
  예시: 점토로 만든 정육면체를 눌러 구로 만들 수 있습니다. 물질을 더하거나 빼지 않고, 연속적으로 변형시킬 수 있죠. 이것이 바로 위상적 변형, 즉 준동형사상의 대표적인 사례입니다.
  

요약하자면, 기하학은 '정확한 모양'을, 위상수학은 '본질적인 연결 구조'를 연구합니다. 즉, 위상수학은 기하학을 더 추상적이고 유연하게 확장한 학문이라 할 수 있습니다.

위상수학의 다양한 분야

위상수학은 하나의 학문이라기보다 여러 분야의 집합체입니다. 각 분야는 서로 다른 시각에서 공간의 본질을 탐구합니다.

• 기하 위상수학: 공간을 자르지 않고 늘리거나 접는 변형을 통해 변하지 않는 성질을 연구합니다.
• 일반 위상수학 (점집합 위상수학): 열린집합, 닫힌집합, 연속성, 연결성 등 위상공간의 기본 원리를 다룹니다.
• 대수적 위상수학: 대수학의 도구를 이용해 위상적 구조를 분석하고, 공간의 불변량을 계산합니다.
• 미분 위상수학: 미분 개념을 통해 곡면과 공간의 매끄러움을 연구합니다.
• 응용 위상수학: 데이터 과학, 네트워크 분석, 생명공학 등 현실 문제에 위상적 기법을 적용합니다.

위상수학은 단순히 추상적인 이론이 아니라, 형태와 구조를 이해하는 언어입니다. 수학자, 물리학자, 그리고 데이터 과학자들 모두가 이 언어를 통해 세상의 복잡한 패턴을 읽어내고 있습니다.