열지도 닫히지도 않은 집합

위상수학에서는 어떤 집합이 열린 집합도 닫힌 집합도 아닐 수 있다. 이는 그 집합이 두 조건 중 어느 것도 충족하지 않는 경우를 말한다.

즉, 해당 집합이 열린 집합으로 정의되어 있지 않으면서, 동시에 열린 집합의 여집합에도 속하지 않을 때 이런 상황이 발생한다.

따라서 이 집합은 닫힌 집합으로 분류될 수도 없다.

참고: 실수의 표준 위상처럼 익숙한 공간에서는 이러한 집합이 낯설게 느껴질 수 있다. 그러나 다양한 위상 공간에서는 충분히 등장하는 개념이며, 아래 예시는 이를 이해하는 데 도움이 된다.

예시로 살펴보기

집합 X={a,b,c,d}와 위상 T가 다음과 같은 열린 집합을 포함한다고 하자. {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, 그리고 Ø.

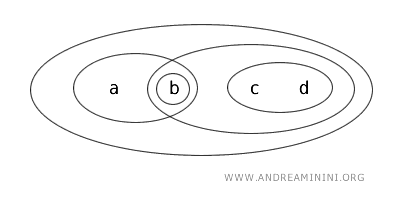
이제 X의 부분집합 {b,c}를 살펴보면 다음과 같은 사실을 확인할 수 있다.

• {b,c}는 위상 T에서 열린 집합으로 정의되지 않았으므로 열린 집합이 아니다.
• {b,c}는 T에 포함된 열린 집합의 여집합도 아니므로 닫힌 집합도 아니다.

결론적으로, 위상 T에서 {b,c}는 열린 집합도 닫힌 집합도 아닌 집합이다.

이러한 구조는 다른 위상 공간에서도 자연스럽게 나타나며, 위상수학에서 집합을 분류할 때 중요한 관점을 제공한다.