위상수학에서의 단일연결공간

위상 공간이 단일연결공간(simply connected)이라 함은, 그 공간 안의 모든 닫힌 경로가 연속적으로 한 점으로 변형될 수 있음을 뜻한다.

쉽게 말해, 공간을 벗어나지 않고 어떤 루프(닫힌 곡선)도 한 점으로 줄일 수 있다면, 그 공간은 단일연결공간이다.

이러한 공간은 내부에 구멍이 없는 하나의 온전한 "덩어리", 즉 연결공간이라 할 수 있다.

참고: 단일연결공간은 언제나 연결공간이지만, 그 반대는 성립하지 않는다. 모든 연결공간이 단일연결인 것은 아니다.

예시로 이해하기

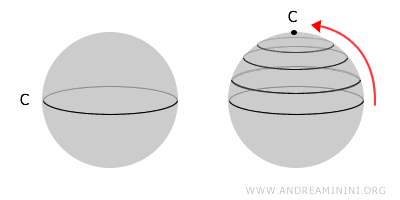
가장 직관적인 예는 구면이다. 구의 표면 위에서는 어떤 닫힌 곡선이라도 연속적으로 줄여서 결국 한 점으로 만들 수 있다. 따라서 구면은 단일연결공간이다.

반대로, 도넛 모양의 토러스(torus)는 중심에 구멍이 있어 그 구멍을 감싸는 루프를 한 점으로 줄일 수 없다. 이런 이유로 토러스는 단일연결공간이 아니다.

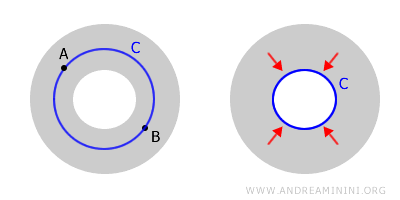
이 예시는 단순히 연결되어 있다고 해서 단일연결임을 보장하지는 않는다는 점을 명확히 보여준다.

도넛 형태의 공간에서는 내부의 어떤 두 점 A와 B를 공간을 벗어나지 않고 하나의 경로로 연결할 수 있으므로 연결공간이다.

그러나 모든 닫힌 곡선을 한 점으로 수축할 수 없기 때문에 단일연결공간은 아니다.

이처럼 연결되어 있지만 단일연결이 아닌 공간을 다중연결공간(multiply connected space)이라고 한다. 대표적인 예로는 고리형 영역과 토러스 공간이 있다.

결국 단일연결성은 호연결성보다 더 강한 성질이다. 단일연결공간의 개념은 위상수학에서 공간의 구조와 형태를 이해하는 데 핵심적인 역할을 하며, 기하학과 물리학 등 여러 분야에서도 중요한 의미를 갖는다.