집합의 폐포

위상공간 \( X \)에서 집합 \( A \)의 폐포란, \( A \)를 포함하는 모든 닫힌 집합들의 교집합으로 정의된다. 이 교집합을 보통 \( \text{Cl}(A) \)로 표기한다.

직관적으로 말하면, 집합 \( A \)의 폐포는 \( A \)를 완전히 포함하는 닫힌 집합들 가운데 가장 작은 닫힌 집합이다.

즉, \( A \)를 포함하는 어떤 닫힌 집합도 그 폐포보다 더 작을 수는 없다.

Note: 이는 폐포의 정의에서 자연스럽게 따라온다. 폐포는 \( A \)를 포함하는 모든 닫힌 집합들의 교집합이므로, \( A \)를 가장 촘촘하게 감싸는 닫힌 집합이라 볼 수 있다. 다시 말해, \( A \)를 포함하는 모든 닫힌 집합에 공통으로 속하는 점들의 집합이 바로 폐포이다.

이를 수식으로 나타내면 다음과 같다.

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ and } C \text{ is closed in } X \} $$

여기서 \( \bigcap \)는 \( A \)를 포함하는 모든 닫힌 집합 \( C \)들의 교집합을 의미한다.

집합 \( A \)의 폐포에는 \( A \)에 속한 점들뿐만 아니라, 위상공간 \( X \)에서 \( A \)의 모든 극한점(또는 축적점)도 함께 포함된다.

Note: 중요한 점은 폐포가 집합 \( A \) 자체의 성질이라기보다, \( A \)가 놓여 있는 위상공간 \( X \)의 위상 구조에 의해 결정된다는 사실이다. 따라서 같은 집합이라도 서로 다른 위상공간에 놓이면 폐포는 달라질 수 있다.

설명 예시

실수 집합 \( \mathbb{R} \)에 표준 위상을 부여하고, 집합 \( A = (0, 1) \)을 생각해 보자.

이는 0과 1 사이의 모든 실수를 포함하되, 양 끝점 0과 1은 포함하지 않는 열린 구간이다.

이 경우 집합 \( A \)의 폐포는 다음과 같다.

$$ \text{Cl}(A) = [0,1] $$

즉, 원래의 열린 구간 \( (0,1) \)에 더해, 경계에 위치한 두 극한점 0과 1이 함께 포함된다.

Note: \( \mathbb{R} \)의 표준 위상에서 닫힌 집합이란 모든 극한점을 포함하는 집합이다. 어떤 점이 극한점이라는 것은, 그 점의 임의의 근방이 집합의 다른 점을 적어도 하나 이상 포함한다는 뜻이다. 예를 들어, 닫힌 구간 [0,2]와 [-1,1]의 교집합은 [0,1]이다. $$ [0,2] \cap [-1,1]=[0,1] $$ 열린 구간 (0,1)을 포함하는 닫힌 집합 중 이보다 더 작은 집합은 존재하지 않는다.

예제 2

이번에는 표준 위상을 갖는 \( \mathbb{R} \)에서 집합 \( A = [0,1) \)을 살펴보자.

이 집합은 0은 포함하지만 1은 포함하지 않는 반열린 구간이다.

이 경우에도 폐포는 동일하다.

$$ \text{Cl}(A) = [0,1] $$

이는 0은 이미 집합 \( A \)에 속해 있고, 1은 집합 \( A \)에는 속하지 않지만 극한점이기 때문이다.

따라서 [0,1]은 \( A \)를 포함하는 가장 작은 닫힌 집합이 된다.

Note: 이 결과는 폐포가 집합의 모든 축적점을 포함한다는 일반적인 원칙과 정확히 일치한다.

예제 3

이제 같은 집합 \( A = [0,1) \)을 이산 위상을 갖는 공간 \( X \)에서 살펴보자.

이산 위상에서는 위상공간의 모든 부분집합이 열린 집합이면서 동시에 닫힌 집합이다.

• 열린 집합
  이산 위상에서는 \( X \)의 모든 부분집합이 열린 집합이다. 따라서 \( A \) 역시 열린 집합이다.
• 닫힌 집합
  모든 부분집합의 여집합 또한 열린 집합이므로, 모든 부분집합은 닫힌 집합이기도 하다. 따라서 \( A \)는 닫힌 집합이다.

이처럼 동시에 열린 집합이자 닫힌 집합인 경우를 클로픈 집합(clopen set)이라 한다.

그 결과, 집합 \( A \)의 폐포는 추가적인 점을 포함할 필요가 없으며, 단순히 \( A \) 자체가 된다.

$$ \text{Cl}(A) = [0,1) $$

Note: 이 예시는 위상의 선택이 폐포의 성질에 얼마나 큰 영향을 미치는지를 잘 보여준다.

예제 4

마지막으로, 점들의 집합 \( \{a, b, c\} \)로 이루어진 위상공간 \( X \)에 이산 위상을 부여해 보자.

이산 위상에서는 다음과 같은 성질이 성립한다.

• \( \emptyset \)와 \( \{a, b, c\} \)는 열린 집합이다.
• 각 점으로 이루어진 집합 \( \{a\} \), \( \{b\} \), \( \{c\} \) 역시 열린 집합이다.
• 이들의 모든 조합인 \( \{a, b\} \), \( \{a, c\} \), \( \{b, c\} \) 또한 열린 집합이다.

여집합 역시 열린 집합이므로, 이산 위상에서는 모든 부분집합이 닫힌 집합이기도 하다.

즉, 이산 위상에서는 모든 집합이 열린 동시에 닫힌 집합이다.

이제 집합 \( A = \{b, c\} \)를 고려하면, 이 집합은 열린 집합이자 닫힌 집합이다.

따라서 \( A \)의 폐포는 추가적인 점을 포함할 필요가 없으며, 다음과 같다.

\[ Cl(A) = \{b, c\} \]

이 경우 모든 집합이 이미 완결된 상태이므로, 별도의 폐쇄 과정이 필요하지 않다.

Note: 실제로 \( A \)를 포함하는 닫힌 집합은 \( \{b, c\} \)와 \( \{a, b, c\} \)뿐이며, 이들의 교집합은 $$ \{b,c\} \cap \{a,b,c\} = \{b, c\} $$ 이다. 따라서 \( Cl(A) = A \)임을 쉽게 확인할 수 있다.

집합의 폐포 정리

위상공간 \( X \)에서 부분집합 \( S \)의 폐포 \( \text{Cl}(S) \)에 한 점 \( y \)가 속한다는 것은, \( y \)를 포함하는 모든 열린 집합 \( U \)가 반드시 \( S \)와 공집합이 아닌 교집합을 가진다는 것과 정확히 같다. 즉 다음과 같은 동치가 성립한다. \( y \in \text{Cl}(S) \iff \forall \ U \text{ (열린 집합)},\ y \in U \Rightarrow U \cap S \neq \emptyset \).

좀 더 쉽게 말하면, 위상공간 \( X \)에서 어떤 점 \( y \)가 집합 \( S \)의 폐포에 속하려면, \( y \)를 포함하는 열린 집합을 어떻게 잡더라도 그 안에는 항상 \( S \)의 점이 하나 이상 존재해야 한다.

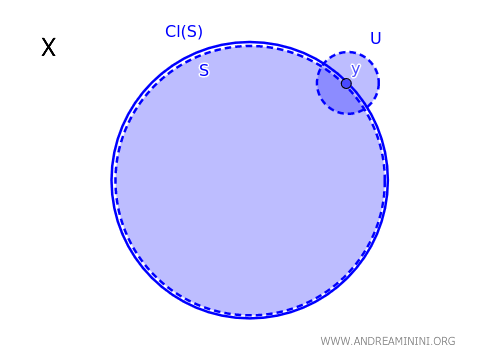
이 정리는 위상공간에서 한 점이 주어진 집합의 폐포에 포함되는지를 판별할 수 있게 해 주는 핵심적인 기준이다.

증명

• 필요조건: \( y \in \text{Cl}(S) \)라고 하자. 폐포의 정의에 의해, \( y \)는 \( S \)를 포함하는 모든 닫힌 집합의 교집합에 속한다. 이는 곧 \( y \)를 포함하는 임의의 열린 집합이 반드시 \( S \)와 교차해야 함을 의미한다. 폐포는 집합 \( S \)의 모든 점과 모든 극한점을 포함하며, 극한점은 정의상 이를 포함하는 모든 열린 근방이 \( S \)와 만나야 한다.
• 충분조건: 반대로, \( y \)를 포함하는 모든 열린 집합이 \( S \)와 교집합을 가진다고 가정하자. 이 경우 \( y \)는 \( S \)의 극한점이거나 이미 \( S \)의 원소이다. 따라서 정의에 의해 \( y \)는 반드시 \( S \)의 폐포에 속한다.

Note: 이 정리는 집합 위상수학에서 매우 자주 사용된다. 열린 집합과 폐포의 개념을 직접적으로 연결해 주며, 연속성, 수렴, 위상적 성질을 다루는 다양한 논의의 출발점이 된다. 또한 여러 중요한 정리들의 증명에서 기본 도구로 활용된다.

예제

실수 집합 \( \mathbb{R} \)에 표준 위상을 부여하고, 열린 구간 \( A = (0, 2) \)를 생각해 보자.

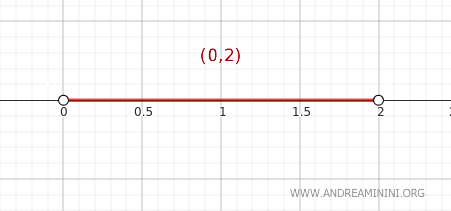
이제 폐포 정리를 이용하여 한 점 \( y \)가 집합 \( A \)의 폐포 \( \text{Cl}(A) \)에 속하는지를 판단해 보자.

예를 들어, 실수 \( y = 2 \)를 고려한다.

정리에 따르면, \( y \in \text{Cl}(A) \)가 성립하려면 \( y \)를 포함하는 모든 열린 집합 \( U \)가 \( A \)와 교집합을 가져야 한다.

1. \( y \)를 포함하는 열린 집합의 확인: \( y = 2 \)를 포함하는 열린 구간 \( (1.9, 2.1) \), \( (1.95, 2.05) \), \( (1.99, 2.01) \) 등을 생각하면, 이들 모두는 \( A = (0,2) \)에 속하는 점들을 포함한다.
2. 결론: \( y = 2 \)를 포함하는 모든 열린 집합이 \( A \)와 교차하므로, 정리에 의해 \( y = 2 \)는 \( \text{Cl}(A) \)에 속한다.

따라서 다음이 성립한다.

$$ y \in \text{Cl}(A) $$

실제로 집합 \( A \)의 폐포는 닫힌 구간 \( \text{Cl}(A) = [0,2] \)이며, 이 안에는 점 \( y = 2 \)가 포함된다.

위상공간에서의 폐포의 기본 성질

이제 위상공간에서 집합의 폐포가 가지는 몇 가지 중요한 성질과, 내부 연산과의 관계를 살펴보자. 이 성질들은 위상수학의 구조를 이해하는 데 핵심적인 역할을 한다.

• 여집합의 내부와 폐포의 여집합
  집합 \( A \)의 여집합의 내부는 \( A \)의 폐포의 여집합과 같다. 즉 $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$
• 여집합의 폐포와 내부의 여집합
  집합 \( A \)의 여집합의 폐포는 \( A \)의 내부의 여집합과 일치한다. $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$

주요 정리와 관찰

다음은 폐포와 관련하여 특히 자주 활용되는 핵심적인 성질들이다.

• C가 닫힌 집합이고 A ⊆ C이면, Cl(A) ⊆ C이다
  \( C \)가 닫힌 집합이고 \( A \subseteq C \)라면, \( A \)의 폐포 역시 \( C \)의 부분집합이다. 이는 폐포가 \( A \)를 포함하는 가장 작은 닫힌 집합이기 때문이다.
• A ⊆ B이면, Cl(A) ⊆ Cl(B)이다
  포함 관계는 폐포 연산에 대해서도 보존된다. 즉 \( A \subseteq B \)이면 \( \text{Cl}(A) \subseteq \text{Cl}(B) \)이다.
• 집합 A는 A = Cl(A)일 때 그리고 그때에 한해 닫힌 집합이다
  집합이 자신의 모든 극한점을 포함할 때, 그리고 그때에만 닫힌 집합이 된다.
• 집합의 폐포는 집합과 그 극한점들의 합집합이다
  집합 \( A \)와 그 극한점들의 집합 \( A' \)에 대해 $$ \text{Cl}(A) = A \cup A' $$
• 멱등성
  폐포 연산을 반복해도 결과는 변하지 않는다. $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$
• 포함 성질
  어떤 집합이든 항상 자신의 폐포에 포함된다. $$ A \subseteq \text{Cl}(A) $$

계속된다.