위상수학에서의 고정점

위상수학에서 고정점은 어떤 함수가 작용하더라도 값이 변하지 않고 그대로 남는 점을 뜻한다.

함수 f(x)가 있을 때 f(p) = p를 만족하는 p가 고정점이다. 즉 p를 입력하면 함수의 결과도 p가 되어, 입력과 출력이 완전히 일치하는 지점이 된다.

$$ f(p) = p $$

이 개념을 직관적으로 이해하려면, 한 점 P를 중심으로 물체를 회전시키는 장면을 떠올려 보면 된다.

회전이 일어나면 물체 위의 다른 점들은 새로운 위치로 이동하지만, 중심점 P만은 제자리에서 변하지 않는다.

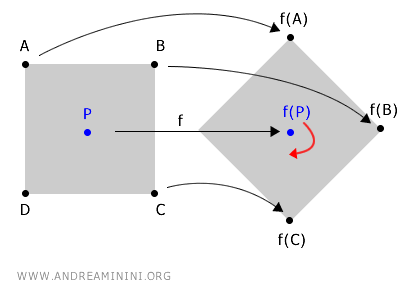
이처럼 회전 중심 P는 어떤 회전 함수 f가 적용되어도 좌표가 그대로 유지되기 때문에 고정점이라고 부른다.

$$ f(P) \longrightarrow P $$

고정점은 단순한 정의를 넘어, 수치해석, 게임 이론, 경제학 등 다양한 분야에서 핵심 개념으로 활용된다. 특히 위상수학에서는 브라우어 고정점 정리로 대표되는 중요한 이론적 기반이 된다.

고정점 예시

닫힌 구간 [0, 2π]에서 f(x) = sin(x)를 생각해 보자.

$$ f(x) = \sin(x) $$

sin(0) = 0이므로 p = 0 라디안은 고정점임을 바로 확인할 수 있다.

$$ \sin(0) = 0 $$

이 경우 입력값과 출력값이 정확하게 일치한다는 점이 고정점의 핵심이다.

예시 2

이번에는 같은 구간 [0, 2π]에서 f(x) = cos(x)를 살펴보자.

$$ f(x) = \cos(x) $$

x = 0은 고정점이 아니다. cos(0) = 1이 되어 입력과 출력이 서로 다르기 때문이다.

하지만 f(x) = cos(x)는 약 x = 0.73908513에서 고정점을 가진다.

$$ \cos(0.73908513) = 0.73908513 $$

이 값은 고정점이 실제로 존재함을 보여 주는 대표적인 예이며, 계산으로 근사할 수 있다는 점에서 실용적인 의미도 크다.

브라우어 고정점 정리

브라우어 고정점 정리는 고정점 이론에서 가장 유명한 결과 중 하나다. 이 정리는 다음 내용을 담고 있다.

연속 함수가 닫힌 n차원 구간을 자기 자신으로 사상할 때, 반드시 하나 이상의 고정점이 존재한다.

이 정리는 고정점이 실제로 어디에 있는지를 찾는 방법을 알려주지는 않지만, 고정점이 반드시 존재한다는 사실을 보장한다는 점에서 매우 중요한 의미를 지닌다.

이 원리는 동역학계의 평형 상태나 경제학의 균형 존재 증명 등 다양한 분야에서 핵심적인 역할을 한다.

고정점 개념은 단순한 정의를 넘어, 수학적 사고를 확장하고 현실 문제를 분석하는 데에도 중요한 도구로 이어진다.