직사각형 기저를 갖는 위상

직사각형 기저를 갖는 위상은 R² 평면을 이해하는 데 매우 직관적인 접근을 제공한다. 이 위상에서는 열린집합을 열린 직사각형들의 합집합으로 설명하며, 각 직사각형은 두 좌표축 방향으로 놓인 열린구간의 데카르트 곱으로 구성된다. 이렇게 단순한 구조는 이차원 공간의 국소적 성질을 파악하는 데 특히 유용하다.

이 위상은 직사각형 열린 근방들로 이루어진 기저(base)를 바탕으로 하며, 이러한 직사각형들이 복잡한 열린집합을 만드는 기본 요소로 작용한다. 기저 개념은 위상론의 핵심 개념이며, 이 경우 직사각형들이 바로 그 역할을 담당한다.

좀 더 구체적으로 말하면, 집합 \( U \subseteq \mathbb{R}^2 \)가 열린집합이 되기 위해서는 다음 조건을 만족해야 한다. \( U \) 안의 임의의 점 \( (x, y) \)에 대해, 그 점을 포함하면서 전체가 \( U \) 내부에 완전히 들어가는 열린 직사각형이 하나 존재해야 한다는 점이다.

이처럼 열린 직사각형은 유클리드 평면 위상을 이해하는 데 기본이 되는 기저 요소로서 매우 중요한 의미를 가진다.

$$ B = \{ (a, b) \times (c, d) \mid a< b,\ c

\( a, b, c, d \)는 실수이며, \( a < b \)와 \( c < d \)는 직사각형을 이루는 두 열린구간의 경계를 설정한다.

직사각형 기저는 보통 열린 원판을 이용해 정의하는 표준 유클리드 위상과 동일한 위상을 만들어낸다. 즉, 기저의 모양이 다르더라도 생성되는 위상 구조는 변하지 않는다.

Note: 위상 구조는 기저의 형태에 의존하지 않는다. 원이든 직사각형이든, 해당 기저가 동일한 열린집합 체계를 만들어낸다면 위상 역시 동일하다. 중요한 것은 도형의 종류가 아니라 그 도형들이 만들어내는 열린집합의 체계다.

직사각형 기저를 이해하기 위한 예

\( \mathbb{R}^2 \)에서 열린 직사각형은 두 축 위에서 정의된 열린구간의 데카르트 곱으로 구성된다. 이 구조는 위상론을 처음 접하는 사람도 쉽게 접근할 수 있는 간단하고 명확한 예다.

예를 들어 보자. \( x \)-축의 열린구간 \( (1, 3) \)과 \( y \)-축의 열린구간 \( (2, 4) \)을 생각해보면, 이 두 구간을 곱해 얻는 직사각형은 다음과 같다.

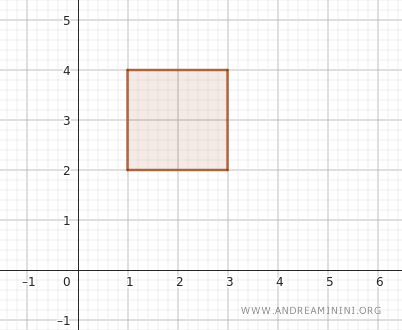
이 직사각형에는 \( x \)가 1보다 크고 3보다 작은 모든 점, 그리고 \( y \)가 2보다 크고 4보다 작은 모든 점이 포함된다. 즉, 점 \( (x, y) \)가 이 범위 안에 있다면 이 열린 직사각형의 내부 점이다.

형식적으로는 \( (1, 3) \times (2, 4) \)로 표현된다.

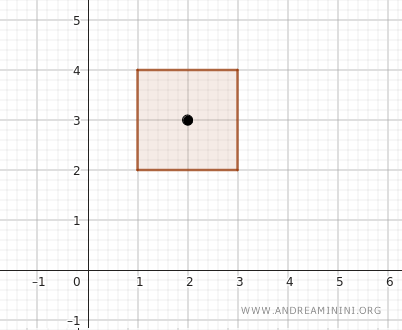
예를 들어 \( (2, 3) \)을 선택하면, 이 점의 \( x \)-좌표는 1과 3 사이에 있고 \( y \)-좌표는 2와 4 사이에 있다는 것을 쉽게 확인할 수 있다. 이 점이 열린 직사각형 내부에 있다는 뜻이다.

Note: 열린 직사각형의 경계는 포함되지 않는다. 따라서 \( (1, y) \), \( (3, y) \), \( (x, 2) \), \( (x, 4) \)와 같은 경계점들은 열린집합의 조건을 만족하지 않는다. 이 점은 열린집합의 정의와 정확히 일치한다.