두 집합 내부들의 합집합
두 집합 $ A $와 $ B $의 내부들의 합집합은 항상 두 집합의 합집합의 내부에 포함된다. \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] 다만 이 포함 관계가 언제나 등식으로 성립하는 것은 아니다.
이 성질은 위상수학에서 자주 등장하는 기본적인 사실로, 각 집합의 내부를 먼저 취한 뒤 이를 합치면 그 결과가 전체 합집합의 내부 안에 반드시 들어간다는 점을 말해 준다.
하지만 두 집합이 항상 정확히 같아지는 것은 아니다. 다시 말해, 다음과 같은 등식은 일반적으로 성립하지 않는다.
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
즉, 포함 관계는 성립하더라도 등호까지 항상 성립하는 것은 아니다.
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
이 차이를 이해하는 것은 집합의 구조와 내부 개념이 어떻게 상호작용하는지를 파악하는 데 매우 중요하다.
구체적인 예
표준 위상을 갖는 실수 공간 \(\mathbb{R}\)에서 두 열린 구간 \( A \), \( B \)를 생각해 보자.
$$ A = (0, 2) $$
$$ B = (1, 3) $$
열린 구간은 열린 집합이므로, 각 구간의 내부는 구간 자체와 같다.
$$ \text{Int}(A) = (0, 2) $$
$$ \text{Int}(B) = (1, 3) $$
따라서 내부들의 합집합은 다음과 같이 주어진다.
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (1, 3) $$
두 구간은 서로 겹치므로, 그 합집합은 하나의 열린 구간으로 정리된다.
$$ (0, 2) \cup (1, 3) = (0, 3) $$
한편 집합 \( A \)와 \( B \)의 합집합 역시
$$ A \cup B = (0, 3) $$
이며, 이 합집합의 내부는 다음과 같다.
$$ \text{Int}(A \cup B) = \text{Int}((0, 3)) = (0, 3) $$
이제 두 결과를 비교하면 다음을 확인할 수 있다.
$$ \text{Int}(A) \cup \text{Int}(B) = (0, 3) $$
$$ \text{Int}(A \cup B) = (0, 3) $$
즉, 이 예에서는 내부들의 합집합과 합집합의 내부가 서로 일치한다.
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
하지만 이러한 결과가 항상 성립하는 것은 아니다.
예를 들어 다음과 같은 두 닫힌 구간을 생각해 보자. $$ A = [0, 2] $$ $$ B = [2, 3] $$ 각 집합의 내부는 $$ \text{Int}(A) = (0, 2), \quad \text{Int}(B) = (2, 3) $$ 이때 합집합 $ A \cup B = [0, 3] $의 내부는 $$ \text{Int}(A \cup B) = (0, 3) $$ 이 경우에도 포함 관계는 성립한다. $$ (0, 2) \cup (2, 3) \subseteq (0, 3) $$ 즉, $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ 하지만 등호는 성립하지 않는다. 실제로 점 $ 2 $는 $$ 2 \in \text{Int}(A \cup B) = (0, 3) $$ 이지만, $$ 2 \notin \text{Int}(A), \quad 2 \notin \text{Int}(B) $$ 따라서 $$ 2 \notin \text{Int}(A) \cup \text{Int}(B) = (0, 2) \cup (2, 3) $$ 결과적으로 $$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
예제 2
이번에는 서로 겹치지 않는 두 열린 구간을 살펴보자.
$$ A = (0, 1) $$
$$ B = (2, 3) $$
이 경우에도 두 집합은 열린 집합이므로, 내부는 각각 구간 자체이다.
$$ \text{Int}(A) = (0, 1) $$
$$ \text{Int}(B) = (2, 3) $$
따라서 내부들의 합집합과 합집합의 내부는 모두
$$ (0, 1) \cup (2, 3) $$
로 주어지며, 이 경우에는 등식이 성립한다.
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
예제 3
마지막으로 표준 위상을 갖는 실평면 \(\mathbb{R}^2\)에서 두 열린 집합 \( A \), \( B \)를 고려하자.
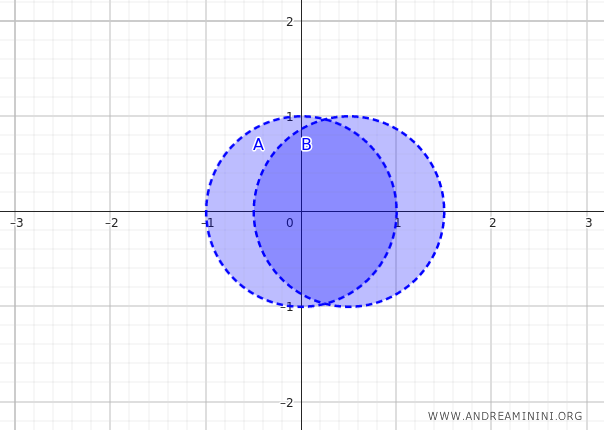
집합 \( A \)와 \( B \)는 각각 중심이 \( (0,0) \), \( (0.5,0) \)이고 반지름이 1인 두 열린 원판이다.
$$ A = \{ (x, y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \in \mathbb{R}^2 \mid (x - 0.5)^2 + y^2 < 1 \} $$
열린 집합의 경우 내부는 집합 자체이므로
$$ \text{Int}(A) = A, \quad \text{Int}(B) = B $$
따라서
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
이 경우에도 마찬가지로 다음 포함 관계가 성립한다.
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
증명
이제 일반적인 경우에 대해 다음 포함 관계를 증명해 보자.
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
집합 \( X \)의 내부 \(\text{Int}(X)\)는, \( X \) 안에 완전히 포함되는 근방을 갖는 모든 점들의 집합으로 정의된다.
\( x \in \text{Int}(A) \cup \text{Int}(B) \)라고 하면, \( x \)는 \(\text{Int}(A)\) 또는 \(\text{Int}(B)\) 중 하나에 속한다.
- \( x \in \text{Int}(A) \)인 경우, \( x \)를 포함하고 \( A \)에 완전히 포함되는 근방이 존재한다.
- \( x \in \text{Int}(B) \)인 경우, \( x \)를 포함하고 \( B \)에 완전히 포함되는 근방이 존재한다.
어느 경우이든 해당 근방은 \( A \cup B \)에 포함된다.
따라서 \( x \)는 \( A \cup B \)의 내부점이며, 이는 곧
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
임을 의미한다. 이로써 증명이 끝난다.