위상수학에서의 항상사상(Homeomorphism)

항상사상(homeomorphism)은 위상수학에서 정의되는 변환으로, 전단사적(bijective)이고 연속이며 그 역함수 또한 연속인 함수를 말한다.

즉, 어떤 공간을 끊거나 붙이지 않고 다른 공간으로 부드럽게 변형했다가 다시 원래 형태로 되돌릴 수 있는 변환이다.

간단히 말하면, 항상사상은 공간을 찢거나 붙이지 않고 자연스럽게 형태를 바꾸는 방법이다.

예를 들어, 손잡이가 달린 커피잔과 도넛(토러스)은 위상수학적으로 항상사상 관계에 있다. 두 도형은 서로를 연속적으로 변형시킬 수 있으며, 그 과정에서 끊어지거나 이어붙는 부분이 전혀 없다.

위상수학적 관점에서 두 도형은 동일한 구조를 갖는다. 왜냐하면 둘 다 ‘구멍이 하나’라는 공통된 위상적 특성을 지니기 때문이다. 도넛의 가운데 구멍과 커피잔 손잡이의 틈은 위상적으로 동일한 역할을 한다. 손잡이 부분을 중심으로 커피잔의 형태를 부드럽게 바꾸면 도넛 모양으로 만들 수 있다.

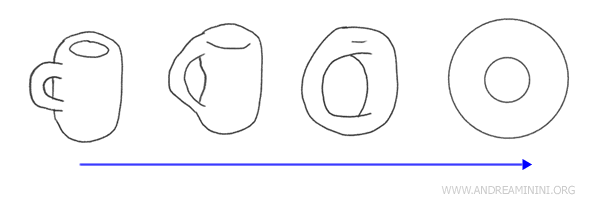
두 위상공간이 항상사상으로 연결되어 있다면, 이들은 항상사상 공간(homeomorphic spaces)이라 부르며, 기하학적으로는 달라 보일지라도 위상수학적으로는 본질적으로 동일한 공간이다.

항상사상의 주요 성질

항상사상이 가지는 핵심적인 성질은 다음과 같다.

• 전단사 함수
  두 공간의 원소 사이에 일대일 대응 관계를 만든다. 즉, 한 공간의 각 원소는 다른 공간의 정확히 하나의 원소에 대응한다.
• 연속성
  항상사상은 연속적인 함수이다. 입력의 작은 변화가 출력의 작은 변화를 유도한다.
• 연속인 역함수
  항상사상의 역함수 또한 연속이어야 하며, 이를 통해 변환이 끊김 없이 되돌릴 수 있다.
• 위상적 성질의 보존
  연속성, 연결성, 콤팩트성과 같은 위상적 성질이 변환 후에도 유지된다. 즉, 원래 공간의 구조적 관계가 변형된 공간에서도 그대로 보존된다.

따라서 항상사상은 두 위상공간 \(X\)와 \(Y\) 사이의 연속적이고 가역적인 대응관계이다. 역함수 또한 연속이므로 두 공간의 위상적 성질이 동일하게 유지된다.

즉, 항상사상은 공간을 찢거나 붙이지 않고 재구성하는 과정으로, 두 도형 또는 공간 사이의 ‘완벽한 대응’을 의미한다.

위상수학에서의 연속성 정의를 다시 살펴보자.

두 위상공간 \(X\)와 \(Y\)가 주어졌을 때, 함수 \(f: X \to Y\)가 연속이라 함은 \(Y\)의 모든 열린집합 \(V\)에 대해 그 역상 \(f^{-1}(V)\)이 \(X\)의 열린집합일 때를 말한다.

즉, 위상수학에서의 연속 함수는 한 공간의 열린집합 구조를 다른 공간으로 옮길 때 그 구조를 유지한다.

따라서 위상수학의 연속성은 해석학에서의 거리 개념에 기반한 연속성보다 훨씬 일반적이고 추상적인 개념이다.

참고: 해석학에서 연속성은 점 사이의 거리 개념에 의존하지만, 위상수학에서는 거리 개념이 필요 없는 열린집합의 구조에 의존한다.

예시를 통한 이해

열린집합을 이용해 항상사상과 연속성의 개념을 시각적으로 이해해 보자.

두 위상공간 \(X = \{a, b, c, d\}\)와 \(Y = \{1, 2\}\)를 고려하자.

• 공간 \(X\)의 열린집합: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\)
• 공간 \(Y\)의 열린집합: \(\{\}, \{1\}, \{1, 2\}\)

함수 \(f: X \rightarrow Y\)가 연속이라는 것은 \(Y\)의 열린집합의 역상이 \(X\)에서 열린집합임을 의미한다.

이제 다음과 같이 함수를 정의하자.

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\)

이 함수를 시각적으로 표현하면, 열린집합을 원으로 표시하여 다음과 같이 나타낼 수 있다.

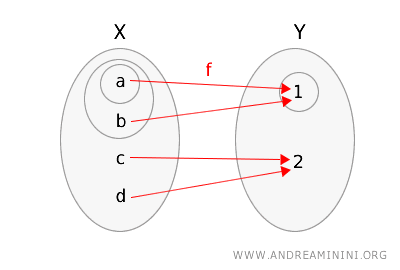
이 함수가 위상적 연속성의 정의를 만족하는지 확인해 보자.

• \(Y\)의 열린집합 \(\{1\}\)의 역상은 \(f^{-1}(\{1\}) = \{a, b\}\)이다. 이 집합은 \(X\)에서 열린집합이다.
• \(Y\)의 열린집합 \(\{1, 2\}\)의 역상은 \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\)이다. 이 역시 \(X\)에서 열린집합이다.

따라서 \(Y\)의 모든 열린집합에 대한 역상이 \(X\)에서 열린집합이므로, 이 함수는 연속이다.

참고: 공집합은 모든 위상공간에서 열린집합으로 간주되므로 별도로 고려할 필요가 없다.

이제 다른 함수를 살펴보자. \(g: X \rightarrow Y\)를 다음과 같이 정의하자.

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\)

이를 그림으로 나타내면 다음과 같다.

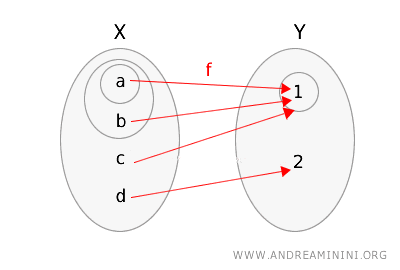
이 함수가 연속인지 확인해 보자.

• \(Y\)의 열린집합 \(\{1\}\)의 역상은 \(g^{-1}(\{1\}) = \{a, b, c\}\)이다. 그러나 이 집합은 \(X\)에서 열린집합이 아니다.

따라서 \(Y\)의 열린집합 중 하나(즉, \(\{1\}\))의 역상이 \(X\)에서 열린집합이 아니므로, 함수 \(g\)는 연속이 아니다.

요약: 목표 공간 \(Y\)의 모든 열린집합에 대해 그 역상이 \(X\)에서 열린집합이면 함수는 연속이다. 그렇지 않다면 연속이 아니다. 위의 예시에서 \(f\)는 모든 열린집합의 역상이 열린집합이므로 연속이고, \(g\)는 그렇지 않으므로 연속이 아니다.

항상사상의 정의

두 위상공간 \( X \)와 \( Y \)가 있고, 전단사 함수 \( f: X \to Y \)와 그 역함수 \( f^{-1}: Y \to X \)가 모두 연속일 때, \( f \)를 항상사상(homeomorphism)이라 한다. 이때 두 공간 \( X \)와 \( Y \)는 항상사상 공간(homeomorphic spaces)이라 하며 \( X \cong Y \)로 표기한다.

항상사상 공간은 위상적으로 동등한 공간(topologically equivalent spaces)이라고도 한다.

그렇다면 이것은 무엇을 의미할까?

항상사상 또는 위상적 동등성은 두 공간이 기하학적으로는 달라도 위상적 관점에서 ‘본질적으로 동일하다’는 의미이다.

이 정의를 통해 항상사상의 핵심 조건을 정리하면 다음과 같다.

1. 전단사성: 함수 \( f: X \to Y \)는 일대일 대응이어야 한다. 즉, \(X\)의 각 원소가 \(Y\)의 정확히 하나의 원소에 대응해야 한다.
2. \( f \)의 연속성: 함수 \( f \)는 연속이어야 하며, 이는 \(Y\)의 열린집합의 역상이 \(X\)에서 열린집합임을 뜻한다.
3. \( f^{-1} \)의 연속성: 역함수 \( f^{-1}: Y \to X \) 또한 연속이어야 하며, 이는 \(X\)의 열린집합의 역상이 \(Y\)에서 열린집합임을 의미한다.

예시: 한 장의 종이를 말아 원통으로 만든다고 생각해 보자. 원통과 평면은 항상사상이다. 왜냐하면 찢거나 붙이지 않고 단순히 말거나 펴는 연속적인 변형으로 서로 변환할 수 있기 때문이다. 기하학적 모양은 다르지만 열린집합의 위상적 구조는 동일하다.

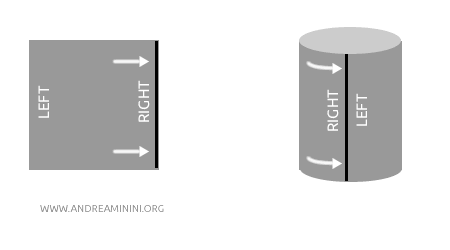
중요한 점은, 전단사 함수 \( f \)가 연속이라고 해서 그 역함수 \( f^{-1} \)이 반드시 연속이라는 보장은 없다는 것이다. 역함수가 연속이 되려면 \( f \)가 열린사상(open map)이어야 한다.

즉, 함수 \( f \)가 연속이고 전단사이더라도, 그 자체로 항상사상임을 보장하지는 않는다. 역함수의 연속성을 위해서는 \( f \)가 열린집합을 열린집합으로 사상하는 열린사상이어야 한다.

예시 1

다음 두 위상공간을 살펴보자.

• \( X = (a, b) \), 위상 \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \)
• \( Y = (1, 2) \), 위상 \( T_Y = \{\emptyset, Y\} \)

함수 \( f: X \to Y \)를 \( f(a) = 1 \), \( f(b) = 2 \)로 정의한다.

이 함수 \( f \)는 \( X \)의 각 원소가 \( Y \)의 정확히 한 원소에 대응하므로 전단사적(bijective)이다.

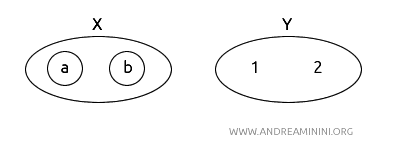
참고: 그림에서 열린집합은 원으로 표시되어 있다. 예를 들어, \( X \)에서는 \(\{a, b\}\), \(\{a\}\), \(\{b\}\)가 열린집합이고, \( Y \)에서는 \(\{1, 2\}\)가 열린집합이다. 공집합은 모든 위상에서 기본적으로 열린집합이므로 생략하였다.

이제 함수 \( f \)와 그 역함수 \( f^{-1} \)의 연속성을 각각 검토해 보자.

• 함수 \( f \)의 연속성
  \( f \)가 연속인지 판단하려면, \( Y \)의 열린집합의 역상이 \( X \)에서 열린집합인지 확인해야 한다. \( Y \)의 열린집합은 \( \emptyset \)과 \( Y \)뿐이다.
  • \( f^{-1}(\emptyset) = \emptyset \) - \( T_X \)에서 열린집합
  • \( f^{-1}(Y) = X \) - \( T_X \)에서 열린집합
  따라서 \( Y \)의 모든 열린집합의 역상이 \( X \)에서 열린집합이므로 \( f \)는 연속이다.
• 역함수 \( f^{-1} \)의 연속성
  역함수 \( f^{-1}: Y \to X \)는 \( f^{-1}(1) = a \), \( f^{-1}(2) = b \)로 정의된다.
  \( f^{-1} \)이 연속이려면, \( X \)의 열린집합의 역상이 \( Y \)에서 열린집합이어야 한다. \( X \)의 열린집합은 \( \emptyset \), \(\{a\}\), \(\{b\}\), \( X \)이다.
  • \( f^{-1}(\emptyset) = \emptyset \) - \( T_Y \)에서 열린집합
  • \( f^{-1}(\{a\}) = \{1\} \) - \( T_Y \)에서 열린집합이 아님. \( Y \)의 유일한 열린집합은 \( Y \) 자신뿐이다.
  • \( f^{-1}(\{b\}) = \{2\} \) - \( T_Y \)에서 열린집합이 아님.
  • \( f^{-1}(X) = Y \) - \( T_Y \)에서 열린집합
  따라서 \(\{a\}\)와 \(\{b\}\)의 역상이 열린집합이 아니므로, 역함수 \( f^{-1} \)은 연속이 아니다.

결론적으로, \( f \)는 전단사이며 연속이지만 역함수 \( f^{-1} \)은 연속이 아니다. 그러므로 \( f \)는 항상사상(homeomorphism)이 아니다.

이 예시는 함수가 전단사이고 연속이더라도, 그 역함수가 반드시 연속일 필요는 없다는 사실을 보여준다.

참고: 이 불연속성은 두 위상공간의 구조적 차이에서 비롯된다. \( X \)는 \(\{a\}\), \(\{b\}\)처럼 더 세밀한(finer) 열린집합을 가지지만, \( Y \)는 \( \emptyset \)과 \( Y \)밖에 없는 더 거친(coarser) 위상을 갖는다.

예시 2

이번에는 다음 두 위상공간을 살펴보자.

• \( X = (a, b) \), 위상 \( T_X = \{\emptyset, \{a\}, X\} \)
• \( Y = (1, 2) \), 위상 \( T_Y = \{\emptyset, \{1\}, Y\} \)

함수 \( f: X \to Y \)를 \( f(a) = 1 \), \( f(b) = 2 \)로 정의한다.

이 경우에도 \( f \)는 전단사이다. \( X \)의 각 원소가 \( Y \)의 유일한 원소에 정확히 대응한다.

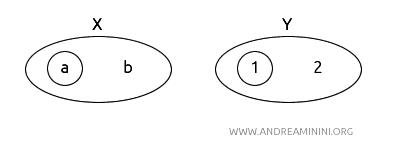
이제 \( f \)와 \( f^{-1} \)의 연속성을 확인해 보자.

• 함수 \( f \)의 연속성
  \( f \)가 연속이려면 \( Y \)의 열린집합의 역상이 \( X \)에서 열린집합이어야 한다. \( Y \)의 열린집합은 \( \emptyset \), \(\{1\}\), \( Y \)이다.
  • \( f^{-1}(\emptyset) = \emptyset \) - \( T_X \)에서 열린집합
  • \( f^{-1}(\{1\}) = \{a\} \) - \( T_X \)에서 열린집합
  • \( f^{-1}(Y) = X \) - \( T_X \)에서 열린집합
  따라서 \( f \)는 연속이다.
• 역함수 \( f^{-1} \)의 연속성
  역함수 \( f^{-1}: Y \to X \)는 \( f^{-1}(1) = a \), \( f^{-1}(2) = b \)이다. \( f^{-1} \)이 연속이려면 \( X \)의 열린집합의 역상이 \( Y \)에서 열린집합이어야 한다. \( X \)의 열린집합은 \( \emptyset \), \(\{a\}\), \( X \)이다.
  • \( f^{-1}(\emptyset) = \emptyset \) - \( T_Y \)에서 열린집합
  • \( f^{-1}(\{a\}) = \{1\} \) - \( T_Y \)에서 열린집합
  • \( f^{-1}(X) = Y \) - \( T_Y \)에서 열린집합
  따라서 \( f^{-1} \) 역시 연속이다.

따라서 \( f \)는 전단사이며 연속이고, 그 역함수 \( f^{-1} \)도 연속이므로 \( f \)는 항상사상이다.

이전 예시와의 차이는 두 공간에 설정한 위상의 구조에 있다.

참고: 이 예시는 위상을 적절히 선택하면 전단사이며 연속인 함수가 연속인 역함수를 가져 항상사상이 될 수 있음을 보여준다. 반면, 위상의 조합이 달라지면 역함수의 연속성이 깨질 수 있다.

항상사상과 다른 위상적 변환의 구별

‘항상사상’이라는 용어는 일반적으로 위상적 변환의 한 형태로 언급되지만, 보다 구체적이고 엄밀한 개념을 가진다.

위상적 변환과 항상사상은 밀접하게 관련되어 있지만 동일한 개념은 아니다.

• 위상적 변환(Topological transformation)
  위상적 변환은 연결성, 연속성 등의 주요 위상적 성질을 보존하면서 공간을 변형시키는 모든 변환을 포함한다. 여기에는 항상사상뿐 아니라 등변형(isotopy), 호모토피(homotopy), 미분동형사상(diffeomorphism) 등이 포함된다.
• 항상사상(Homeomorphism)
  항상사상은 전단사이며 연속이고, 역함수 또한 연속인 특별한 경우의 변환이다. 이러한 변환을 통해 두 공간은 서로 끊김 없이 되돌릴 수 있으며, 위상적으로 동일한 구조를 공유한다.

모든 항상사상은 위상적 변환에 속하지만, 모든 위상적 변환이 항상사상인 것은 아니다. 일부 위상적 변환은 연속성이나 가역성 조건을 만족하지 않아 항상사상이 되지 못한다.

추가 참고사항

항상사상과 관련된 몇 가지 중요한 개념을 정리하면 다음과 같다.

• 위상적 성질(Topological property)
  위상적 성질은 항상사상에 의해 보존되는 공간의 특성을 말한다. 즉, 두 위상공간이 항상사상 관계에 있다면(연속적 일대일 대응과 연속인 역함수가 존재한다면), 두 공간은 동일한 위상적 성질을 공유한다.
• 하우스도르프의 항상사상 정리
  \( f: X \to Y \)가 항상사상이고 \( X \)가 하우스도르프 공간이라면, \( Y \) 역시 하우스도르프 공간이 된다. 이는 항상사상이 위상적 성질을 그대로 보존하기 때문이다.
• 추상대수학에서 항상사상과 유사한 개념은 군 동형사상(group isomorphism)이다. 군 동형사상은 대수적 연산 구조를 보존하는 전단사 함수이며, 항상사상은 열린집합의 구조를 보존한다는 점에서 대응된다.

이처럼 항상사상은 공간의 기하학적 형태가 아니라 위상적 구조의 본질을 이해하는 데 핵심적인 개념이다.