위상의 기저

위상의 기저란 위상 공간 T에서 모든 열린 집합을 기저 B에 속한 집합들의 합집합으로 나타낼 수 있도록 하는 열린 집합들의 모임 B를 말합니다.

집합 X와 그 부분집합들의 모임 T가 X 위의 위상을 이룰 때, 위상 T의 기저 B는 다음 조건을 만족하는 집합들의 모음이며, 각 집합을 기저 원소라고 합니다.

• X의 모든 원소 x는 B의 어떤 집합에 반드시 포함되어야 합니다.
• x가 B의 두 집합 B₁과 B₂의 공집합이 아닌 교집합 B₁∩B₂에 속한다면, 그 교집합 안에는 x를 포함하는 더 작은 기저 집합 B₃가 존재해야 합니다.
  

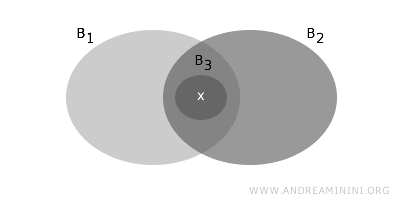
이 조건들은 B가 T의 기저로 기능하기 위해 요구되는 기본 공리 조건들입니다.

왜 중요한가?

기저를 사용하면 위상 T의 열린 집합 전체를 일일이 열거할 필요 없이 기저 원소들의 합집합만으로 위상을 간결하게 기술할 수 있습니다.

Note. 기저 원소들의 교집합 조건은 두 열린 집합의 교집합도 항상 열린 집합이어야 한다는 위상의 핵심 공리를 보장합니다.

예시: 유한 집합에서의 기저

다음 집합 X를 고려합니다.

$$ \{a, b, c \} $$

다음과 같은 위상 T를 정의합니다.

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

T는 X에서 정의된 모든 열린 집합의 모임입니다.

이 위상의 하나의 기저 B는 다음과 같습니다.

$$ B = \{ \{ a \} ,\{ b,c \} \} $$

B는 X={a,b,c}의 모든 원소를 포함하며 기저 조건을 충족합니다.

T의 모든 열린 집합은 B의 원소들만으로 구성됩니다.

$$ \{ a \} \in B $$

$$ \{ b,c \} \in B $$

$$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

Note. 공집합 Ø은 모든 집합의 비진부분집합이며 위상의 기본 공리에 따라 항상 열린 집합입니다. 따라서 B에도 포함됩니다. $$ \emptyset \in B $$

이 예시는 유한한 상황에서 기저가 어떻게 열린 집합을 구성하는지 잘 보여 줍니다.

보다 복잡한 위상이나 무한 집합에서도 기저의 개념은 동일하며, 기저는 위상 공간의 모든 열린 집합을 이루는 기본 구성 단위 역할을 합니다.

다른 기저

X={a,b,c} 위상의 또 다른 기저는 다음과 같습니다.

$$ B = \{ \{ a \} ,\{ b \}, \{ c \} \} $$

이는 X의 각 원소에 대한 단일집합으로 구성된 기저입니다.

기저 B는 위상 T={ Ø,X,{a},{b,c}}를 다음과 같이 생성합니다.

• 공집합 Ø은 정의에 따라 열린 집합입니다.
• {a}는 이미 기저 B에 포함됩니다. $$ \{ a \} \in B $$
• {b,c}는 {b}와 {c}의 합집합입니다. $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
• 전체 집합 X={a,b,c}는 세 단일집합의 합집합입니다. $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

따라서 이 B 역시 T의 모든 열린 집합을 생성하는 기저입니다.

Note. 하나의 위상에는 서로 다른 기저들이 존재할 수 있으며, 각각은 동일한 열린 집합들을 생성하지만 구성 방식은 달라질 수 있습니다.

예시 2: 실수선의 기저

실수선 전체는 a< b인 열린 구간 (a,b)들의 모임으로 덮을 수 있습니다.

$$ B=\{ \ (a,b) ⊂ \ R \ | \ a < b \ \} $$

실수선의 모든 점은 어떤 열린 구간 (a,b)에 포함되므로 이 집합은 실수선의 기저로 적절합니다.

또한 두 열린 구간이 교차할 때, 그 교집합에는 교차점 주변을 포함하는 또 다른 열린 구간이 존재합니다.

예를 들어, (0, 3)과 (2, 4)의 교집합은 (2,3)입니다.

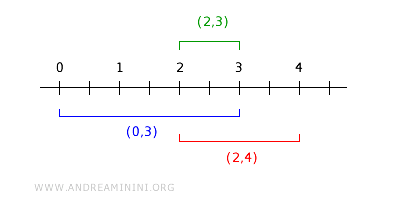
(2,3)은 기저 B의 원소이며 두 구간의 교집합 안에 위치합니다. $$ (0,3) \cap (2,4) = (2,3) ∈  B_i ⊂ (0,3) \cap (2,4) ⊂ B $$

가산 기저(Countable Basis)

가산 기저란 위상 공간 \( X \)에서 모든 열린 집합을 생성하는 기저 \( \mathcal{B} = \{B_1, B_2, B_3, \dots\} \)가 가산 집합을 이루는 경우를 말합니다. 다시 말해, 위상의 열린 집합들이 모두 기저 원소들의 합집합으로 표현되면서, 그 기저가 자연수와 일대일 대응 가능한 열거 가능한 집합일 때 이를 가산 기저라고 합니다.

집합이 가산이라는 것은 그것이 유한 집합이거나, 혹은 그 원소들을 자연수 집합 \( \mathbb{N} \)과 일대일 대응시킬 수 있음을 뜻합니다. 따라서 어떤 집합의 원소를 \( B_1, B_2, B_3, \dots \)와 같이 나열할 수 있다면 그 집합은 가산입니다.

기저와 가산 기저의 차이

모든 기저는 주어진 위상을 생성하지만, 그중에서도 원소들이 가산적인 기저만을 특별히 가산 기저라고 합니다. 이는 단순히 위상이 존재한다는 사실보다 강한 조건이며, 공간의 성질을 더 정밀하게 분석할 수 있게 해줍니다.

왜 중요한가? 가산 기저는 위상수학에서 핵심적인 개념입니다. 예컨대, 우리손 계량 정리(Urysohn’s Metrization Theorem)의 중요한 조건으로 등장하며, 해석학과 위상수학의 여러 정리들은 제2 가산 공간(second-countable space), 즉 가산 기저를 갖는 공간에서만 성립하거나 더욱 단순한 형태를 갖습니다.

예시

표준 위상을 갖는 실수선 \( \mathbb{R} \)에서는 유리수 \( a, b \in \mathbb{Q} \)이면서 \( a < b \)인 모든 열린 구간 \( (a, b) \)들의 모임이 가산 기저를 이룹니다. 이 구간들은 모두 열거 가능하므로 가산 집합을 형성합니다.

증명

자연수 집합은 다음과 같이 순차적으로 나열할 수 있으므로 가산입니다.

\[ 1,\ 2,\ 3,\ 4,\ 5,\ \dots \]

유리수 집합 역시 가산입니다. 예를 들어 다음과 같이 열거할 수 있습니다.

\[ 0,\ 1,\ -1,\ \tfrac{1}{2},\ -\tfrac{1}{2},\ \tfrac{2}{3},\ -\tfrac{2}{3},\ \dots \]

이를 \( q_1, q_2, q_3, \dots \)라 하겠습니다.

이제 가능한 모든 쌍 \( (q_i, q_j) \) 중 \( q_i < q_j \)인 경우를 고려하면, 유리수 끝점을 갖는 모든 열린 구간이 생성됩니다.

예를 들어:

• \( (q_1, q_2) = (0, 1) \)
• \( (q_3, q_2) = (-1, 1) \)
• \( (q_4, q_5) = (\tfrac{1}{2}, -\tfrac{1}{2}) \) ❌ 제외됨. 조건 \( a < b \) 불충족.
• \( (q_5, q_1) = (-\tfrac{1}{2}, 0) \)
• ...

이와 같이 \( q_i < q_j \)을 만족하는 모든 쌍을 나열하면, 다음과 같은 열린 구간 목록을 형성할 수 있습니다.

1. \( (0, 1) \)
2. \( (-1, 1) \)
3. \( (-\tfrac{1}{2}, 0) \)
4. \( (0, \tfrac{1}{2}) \)
5. \( (-1, \tfrac{1}{2}) \)
6. \( (\tfrac{1}{2}, 1) \)
7. \( (-\tfrac{2}{3}, 0) \)
8. \( (0, \tfrac{2}{3}) \)
9. \( (-1, \tfrac{2}{3}) \)
10. \( (-\tfrac{1}{2}, \tfrac{1}{2}) \)
11. ...

결국 유리수 끝점을 갖는 열린 구간들은 무한히 많지만 자연수처럼 열거할 수 있으므로 가산이며, 따라서 이 모임은 실수선의 표준 위상에 대한 가산 기저입니다.

추가 관찰

다음은 기저 구성에 대한 몇 가지 보조적 관찰입니다.

• 집합 X의 각 원소 x에 대해 단일집합 {x}를 기저 원소로 포함하도록 기저 B를 구성하면, X 위의 어떤 위상도 생성할 수 있습니다.

  단일집합들의 합집합을 조합하면 X 위의 모든 가능한 위상을 기술할 수 있습니다.
  
  예를 들어, X={a,b,c}의 기저 B={ {a}, {b}, {c} }는 위상 T={Ø,{a},{b,c},X}를 생성합니다.
  
  동일한 기저 B는 다른 위상들도 생성할 수 있습니다. 예를 들어 T={Ø,{b},{a,c},X}, 자명 위상 T={Ø, X}, 이산 위상 T={Ø,{a},{b},{c},{a,b},{a,c},{b,c},X} 등 다양한 위상을 얻을 수 있습니다.

  Note. 첫 번째 기저 조건은 X의 모든 원소가 단일집합 {x}에 포함되므로 자명하게 충족됩니다. 두 번째 조건 역시 단일집합들이 서로 교차하지 않기 때문에 자동적으로 만족됩니다.

이와 같이 단일집합을 활용하여 기저를 구성하면 X 위의 모든 위상을 생성할 수 있습니다.