열린닫힌집합 (clopen set)
위상공간에서 어떤 집합이 열린 집합(open set)이면서 동시에 닫힌 집합(closed set)일 때, 그 집합을 열린닫힌집합(clopen set, 또는 개폐집합)이라고 한다.
열린닫힌집합은 하나의 위상에서 열린 집합의 조건과 닫힌 집합의 조건을 모두 만족하는 집합이다. 이러한 개념은 두 성질이 어떻게 한 공간 안에서 공존할 수 있는지를 보여 주며, 위상수학에서 공간의 구조를 이해하는 데 중요한 의미를 갖는다.
특정 집합과 그 여집합이 모두 열린 집합으로 정의될 때 열린닫힌집합이 된다. 일반적인 위상에서는 드물지만, 위상 공간의 연결성이나 분해 구조를 분석할 때 핵심적으로 등장한다.
예시
집합 X={a,b,c,d}에 위상 T가 주어져 있다고 하자.
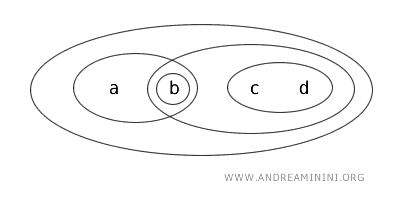
이 위상에서 열린 집합은 {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, 그리고 Ø 이다. 따라서 {a,b}는 위상 T에서 열린 집합이다.
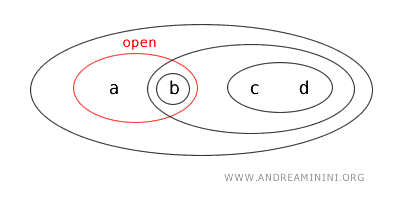
또한 {a,b}는 열린 집합 {c,d}의 여집합이기도 하다.
$$ X - \{ c,d \} = \{a , b \} $$
열린 집합의 여집합은 닫힌 집합이 되므로 {a,b}는 닫힌 집합이기도 하다.
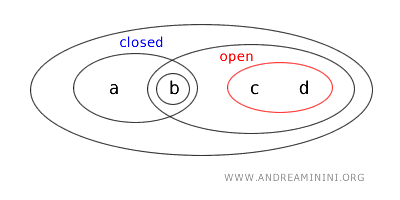
따라서 {a,b}는 열린 집합이면서 닫힌 집합이다. 이러한 집합을 열린닫힌집합이라고 한다.
공집합과 전체집합은 항상 열린닫힌집합
어떤 위상공간에서든 전체집합 X와 공집합 ∅은 항상 열린닫힌집합이다.
먼저, 열린 집합의 정의에 따르면 공집합(∅)과 전체집합(X)은 언제나 열린 집합이다. 이어서 닫힌 집합의 정의에 따르면, 여집합이 열린 집합이면 해당 집합은 닫힌 집합이다.
- 공집합(∅)
공집합은 열린 집합이다. 여집합 X $ \setminus ∅=X $ 또한 열린 집합이므로 닫힌 집합이기도 하다. - 전체집합(X)
전체집합은 열린 집합이다. 여집합 $ X \setminus X=∅ $ 역시 열린 집합이므로 닫힌 집합이기도 하다.
따라서 공집합과 전체집합은 어떤 위상에서나 열린닫힌집합의 대표적인 예가 된다.
열린닫힌집합의 개념을 이해하면 위상 공간의 연결성, 분해 가능성, 그리고 전체 구조를 더욱 깊이 있게 파악할 수 있다. 이는 위상수학을 공부할 때 중요한 출발점이 된다.