정규 위상공간(Normal Topological Space)

위상수학을 살펴보다 보면, 서로 떨어진 두 닫힌집합을 얼마나 "깔끔하게" 분리할 수 있는지가 중요한 기준이 된다. 정규 위상공간은 바로 이러한 분리가 항상 가능한 구조를 갖춘 공간이다. 이 개념은 추상적으로 보일 수 있지만, 실제 예를 통해 보면 그 직관이 명확해진다.

간단히 말해, 정규공간에서는 떨어져 있는 두 닫힌집합을 각각 안전하게 감싸주는 열린집합을 항상 찾을 수 있다. 이러한 구조는 연속함수를 사용해 점들을 구분하는 여러 정리의 기반이 된다.

예시로 이해하는 정규성

대표적인 예로 실수직선 \( \mathbb{R} \)을 떠올려 보자. 표준위상에서는 \( (a, b) \) 형태의 열린구간들이 기본 열린집합을 이룬다.

서로소인 닫힌집합을 다음과 같이 선택해 보자.

• \( A = \{0\} \)
• \( B = [2, 3] \)

두 집합은 모두 닫힌집합이며, 공통 원소가 없으므로 서로소이다.

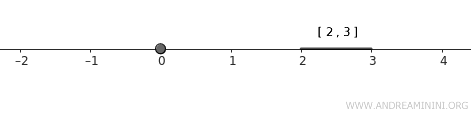
참고. 단일점 집합 \( A \)는 스스로 닫힌집합이며, 닫힌구간 \( B \) 역시 표준위상에서 닫힌집합이다.

이제 각 집합을 포함하는 서로소 열린집합을 찾아보자.

단일점 \( A \)를 감싸는 열린근방으로는 \( U = (-1, 1) \)이 적당하다.

$$ A \subset U = (-1,1) $$

\( B = [2,3] \)을 포함하는 열린근방은 \( V = (1, 4) \)로 잡을 수 있다.

$$ B \subset V = (1,4) $$

이 두 열린집합은 서로 겹치지 않으므로 \( U \cap V = \emptyset \)이 성립한다. 이것만 봐도 실수직선이 정규공간의 조건을 충족한다는 점이 드러난다.

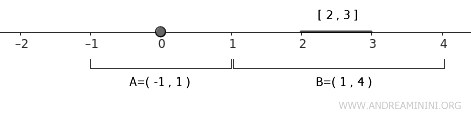
이 원리는 단순한 예시에만 국한되지 않는다. 실수직선 위의 어떤 두 서로소 닫힌집합을 골라도 항상 이와 같은 분리가 가능하다. 이것이 바로 실수직선이 정규공간으로 분류되는 이유다.

정규공간이 중요한 이유

정규공간은 위상수학의 다양한 정리에서 핵심적 조건으로 등장한다. 다음은 그중 자주 언급되는 성질들이다.

• 실수직선 \( \mathbb{R} \)은 정규공간이다
  표준위상을 갖는 \( \mathbb{R} \)은 정칙성보다 더 강한 정규성을 만족한다.
• 모든 거리공간(metric space)은 정규적이다
  거리구조가 주어지면 두 집합을 충분히 벌릴 수 있는 여유가 생기므로 정규성이 자동으로 따라온다.
• 정규공간이면 정칙공간이다
  정규성은 정칙성보다 강한 위상적 성질이다.

정규공간은 Urysohn 보조정리나 Tietze 확장정리처럼 연속함수의 존재를 보장하는 강력한 정리들의 기초가 되므로, 위상수학을 이해하기 위해 반드시 짚고 넘어가야 하는 중요한 개념이다.