부분공간 위상

위상공간 \( (X, T) \)에서 \( X \)는 집합이고 \( T \)는 그 위상을 이루는 열린집합들의 모임이다. 부분집합 \( Y \subseteq X \)가 주어지면, \( Y \)에는 부분공간 위상, 또는 유도위상이 정의된다. 이 위상은 다음과 같이 주어진다. \[
T_Y = \{ U \cap Y \mid U \in T \}. \] 즉 \( Y \)에서의 열린집합은 \( X \)의 열린집합 \( U \)와 \( Y \)의 교집합으로 결정된다.

따라서 집합 \( V \subseteq Y \)가 부분공간 위상에서 열린집합이 되려면, \( X \)의 열린집합 \( U \)가 존재하여 \( V = U \cap Y \)가 되어야 한다. 이 단순한 조건이 부분공간 위상의 핵심이다.

부분공간 위상에서 \( Y \)의 모든 열린집합은 다음과 같은 형태를 가진다.

$$ V_{open \ in \ Y} = U \cap Y $$

닫힌집합 역시 같은 방식으로 정의되며, \( X \)에서 닫힌집합 \( C \)에 대해 다음과 같이 표현된다.

$$ V_{closed \ in \ Y} = C \cap Y $$

결과적으로 위상적 부분공간이란 원래 공간의 위상을 그대로 이어받아 형성되는 부분집합이다.

Note. 부분공간 위상에서 열린집합이라고 해도 \( X \) 전체에서 열려 있지 않을 수 있다. 반대로 \( X \)에서는 닫힌집합이지만 \( Y \)에서는 열린집합이 되는 경우도 있으며, 두 공간에서 모두 열리거나 모두 닫힌 경우도 있다. 열린 동시에 닫힌 집합, 즉 클로펜 집합도 나타난다. 이러한 차이는 부분공간 위상이 원래의 위상 구조를 그대로 반영하면서도, 부분집합의 특성에 따라 달라지기 때문에 생긴다.

예시로 살펴보는 부분공간 위상

표준위상을 갖는 실수공간 \( \mathbb{R} \)을 생각해 보자. 이 공간에서 열린집합은 열린구간이다.

이제 부분집합 \( Y = [0, 1] \)을 선택하자. 부분공간 위상에서 \( Y \)의 열린집합은 모두 다음과 같은 꼴을 갖는다.

$$ U \cap [0, 1] $$

여기서 \( U \)는 \( \mathbb{R} \)에서 열린집합이다. 예를 들어, 구간 \( (-1, 0.5) \)는 \( \mathbb{R} \)에서 분명히 열린집합이다.

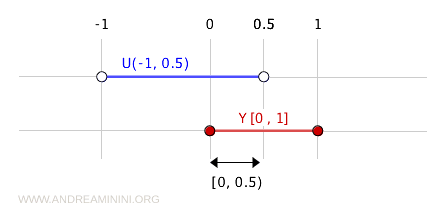
이 열린구간을 \( Y \)와 교집합하면 다음과 같은 집합이 만들어진다.

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

구간 \( [0, 0.5) \)는 \( \mathbb{R} \)에서는 열린집합이 아니지만, 부분공간 \( Y \)에서는 열린집합이 된다. 이는 부분공간 위상의 대표적인 특징이다.

반대로 \( [0, 0.5] \)은 닫힌집합 [-1, 0.5]와의 교집합으로 얻어지므로 부분공간 \( Y \)에서 닫힌집합이다.

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

Note. 구간 [0,a)나 (a,1]처럼 표준위상에서는 반닫힌구간 또는 닫힌집합에 속하는 것들도, 부분공간 \( Y=[0,1] \)에서는 열린집합이 될 수 있다. 이는 이 구간들이 \( \mathbb{R} \)의 열린구간과의 교집합으로 표현되기 때문이다.

예를 들어 (0.2, 0.8)은 부분공간 \( Y \)와 \( \mathbb{R} \) 모두에서 열린집합이며, [0.2, 0.8]은 양쪽에서 모두 닫힌집합이다.

또한 부분공간 \( Y = [0, 1] \)에서는 전체집합 자체가 열린 동시에 닫힌 집합이 된다.

• Open
  \( [0, 1] \)이 부분공간 \( Y \)에서 열린집합임을 보이려면 \( \mathbb{R} \)에서 열린집합 \( U \) 중 \( U \cap Y = [0, 1] \)이 되는 것을 찾으면 된다. \( U = \mathbb{R} \)은 열린집합이므로 $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ 이 된다. 따라서 \( [0, 1] \)은 부분공간 \( Y \)에서 열린집합이다.
• Closed
  \( [0, 1] \)이 부분공간 \( Y \)에서 닫힌집합임을 보이기 위해서는 \( \mathbb{R} \)의 닫힌집합 \( C \) 중 \( C \cap Y = [0, 1] \)이 되는 것을 찾으면 된다. \( C = [0, 1] \)을 사용하면 $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ 이 되어 닫힌집합임을 알 수 있다.

  Note: 부분공간 \( Y \)에서 전체집합의 여집합은 공집합이고, 공집합은 항상 열린집합이다. 따라서 그 여집합인 \( [0,1] \)은 자동으로 닫힌집합이 된다.

결론적으로 부분공간 \( Y = [0, 1] \)에서는 집합 \( [0, 1] \)이 열린 동시에 닫힌, 즉 클로펜 집합이다. 이는 부분공간 위상이 가지는 흥미롭고 중요한 성질 중 하나다.

예제 2

표준위상을 갖는 실수집합 \(\mathbb{R}\)을 떠올려 보자.

이 위상에서는 열린구간 (a, b)과 그들의 합집합이 열린집합을 이룬다. 이러한 구조 속에서 정수집합 \(\mathbb{Z}\)는 흥미로운 부분공간의 예가 된다. 이유는 간단하다. 각 정수는 \(\mathbb{R}\)의 열린구간과 \(\mathbb{Z}\)의 교집합을 통해 하나의 점으로 정확히 분리될 수 있기 때문이다.

예를 들어 정수 7은 다음처럼 표현된다.

$$ (6.5, 7.5) \cap \mathbb{Z} = \{ 7 \} $$

\(\mathbb{Z}\)의 다른 정수들도 같은 방식으로 얻을 수 있다. 이런 이유로 \(\mathbb{Z}\)의 각 원소는 부분공간 위상에서 열린집합이 되며, 결국 \(\mathbb{Z}\)의 모든 부분집합이 열린집합이 된다.

예를 들어 다음과 같이 특정 구간의 정수만을 얻을 수도 있다.

$$ (5.5, 8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

이와 같이 만들어지는 \(\mathbb{Z}\)의 부분공간 위상은 바로 이산위상(discrete topology)으로 알려져 있다.

Note: \(\mathbb{Z}\) 위에 독립적으로 정의될 수 있는 이산위상은 \(\mathbb{R}\)의 표준위상에서 유도되는 부분공간 위상과 위상적으로 일치한다.

예제 3

이번에는 관점을 3차원 유클리드 공간 \(\mathbb{R}^3\)으로 넓혀 보자. 이 공간의 열린집합은 열린볼(open ball)과 그들의 합집합으로 구성된다.

단위구 \( S^2 \)는 다음과 같은 점들의 집합이다.

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

이제 \( S^2 \)에 부분공간 위상을 부여하면 다음과 같이 정의된다.

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{는 } \mathbb{R}^3 \text{의 열린집합} \} $$

즉, \( S^2 \)의 부분집합 \( V \)가 열린집합이 되려면, \(\mathbb{R}^3\)의 열린집합 \( U \)에 대해 \( V = U \cap S^2 \)로 표현될 수 있어야 한다.

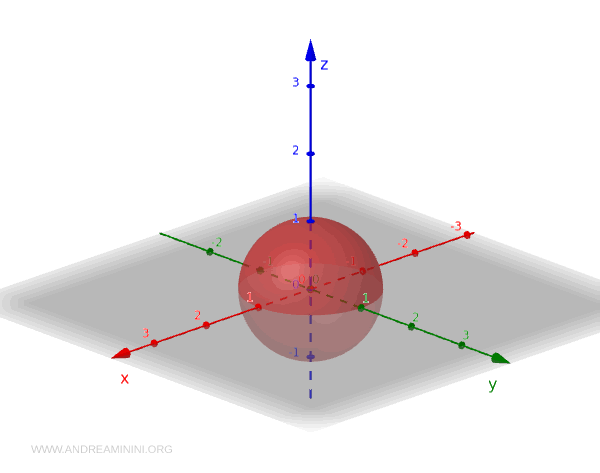
\( S^2 \)에서 열린집합이 구성되는 방식은 다음 예시들을 통해 직관적으로 이해할 수 있다.

• \(\mathbb{R}^3\)의 열린집합과의 교집합
  \( U = \{ (x, y, z) \mid x^2 + y^2 + z^2 < 2 \} \)는 \(\mathbb{R}^3\)의 열린집합이다. 단위구의 모든 점은 반지름 1을 가지므로 이 조건을 만족하며, 그 결과 $$ U \cap S^2 = S^2 $$ 즉, \( S^2 \) 자체가 부분공간 위상에서 열린집합이 된다.
• 구면의 특정 영역
  \( U = \{ (x, y, z) \mid x^2 + y^2 + z^2 = 1 \text{ 그리고 } z > 0 \} \)을 생각해 보자. 이는 단위구의 상반구에 해당한다. $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ 이 영역은 부분공간 위상에서 열린집합이다.
• 열린집합의 기본 성질
  • 공집합과 전체집합 \( S^2 \)는 항상 열린집합이다.
  • 유한 개의 열린집합의 교집합은 열린집합으로 남는다.
  • 임의 개수의 열린집합의 합집합도 열린집합이다.

요약하자면, \( S^2 \)는 \(\mathbb{R}^3\)의 부분공간으로서 표준위상의 구조를 그대로 이어받는다. 따라서 \( S^2 \)에서 열린집합은 언제나 \(\mathbb{R}^3\)의 열린집합과의 교집합으로 표현된다.

부분공간 위상의 핵심 성질

부분공간 위상은 다음과 같은 성질을 통해 전체 위상 구조와 자연스럽게 연결된다.

1. 열린집합의 구조
   \( Y \)에서의 열린집합은 항상 \( U \cap Y \) 형태이며, 여기서 \( U \)는 \( X \)에서 열린집합이다.
2. 공집합과 전체집합
   \( \emptyset \)과 \( Y \)는 부분공간 위상에서 항상 열린집합이다.
3. 유한 교집합
   유한 개의 열린집합의 교집합은 \( X \)에서와 마찬가지로 열린집합이다.
4. 임의 합집합
   임의 개수의 열린집합의 합집합도 열린집합이다.

추가 참고

• \(\mathbb{R}^n\)의 부분집합 \( Y \)에 부여하는 표준위상은 \(\mathbb{R}^n\)에서의 부분공간 위상과 동일하다.

  Example. 집합 \( Y = [-1,0) \cup (0,1] \)을 생각해 보자. 이 집합에서의 표준위상은 \(\mathbb{R}\)의 열린구간과의 교집합을 통해 정의되며, 부분공간 위상과 완전히 일치한다. $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ 두 구간은 Y에서 모두 열린집합이며, 서로의 여집합이므로 동시에 닫힌집합이다. 즉, 두 집합은 Y에서 클로펜(clopen) 집합이다.

• 부분공간 위상의 기저 정리
  위상공간 \( X \)의 기저 \( B_X \)가 주어졌다면, 각 기저 원소와 \( Y \)의 교집합으로 이루어진 집합족은 부분공간 위상의 기저를 이룬다. $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$