경로 연결 공간이란 무엇일까?

경로 연결 공간(path-connected space)이란, 공간 안의 임의의 두 점 A와 B를 그 공간을 벗어나지 않고 하나의 연속적인 경로로 연결할 수 있는 위상 공간 S를 말한다.

한 장의 종이를 떠올려 보자. 모서리를 제외하면 종이는 하나의 끊김 없는 표면이다. 이런 공간은 경계가 포함되지 않으므로 열린(open) 공간으로 본다.

이 종이 위의 두 점 A와 B를 골라 펜을 종이에서 떼지 않은 채 선을 그릴 수 있다면, 그 종이는 바로 경로 연결 공간의 좋은 예다.

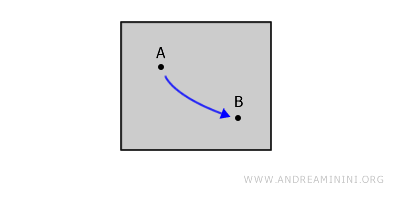
즉, A와 B를 잇는 경로가 존재하며, 그 경로는 결코 종이 밖으로 나가지 않는다.

모든 경로 연결 공간은 연결(connected) 공간이다.

이는 매우 직관적이다. 공간이 만약 분리되어 있다면, 즉 서로 떨어진 부분으로 나뉘어 있다면, 두 점을 연속적인 경로로 연결할 수 없을 것이기 때문이다.

하지만 반대로, 연결되어 있다고 해서 반드시 경로 연결인 것은 아니다. 이것이 바로 흥미로운 부분이다.

이제 다소 직관에 반하지만 수학적으로 중요한 예시를 살펴보자.

다음의 두 집합 Q와 T를 생각해 보자.

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

집합 Q는 0을 제외한 모든 실수에서 정의된 함수 sin(1/x)의 그래프 위의 점들로 구성되어 있다. x가 0에 가까워질수록 사인파는 점점 더 빠르게 진동하지만, x=0에서는 정의되지 않는다.

집합 T는 단 하나의 점, 0만을 포함한다.

이 두 집합 Q와 T는 서로 무한히 가까이 있다. 아래의 그래프를 보면 sin(1/x)의 진동이 0 근처에서 점점 조밀해지는 모습을 확인할 수 있다.

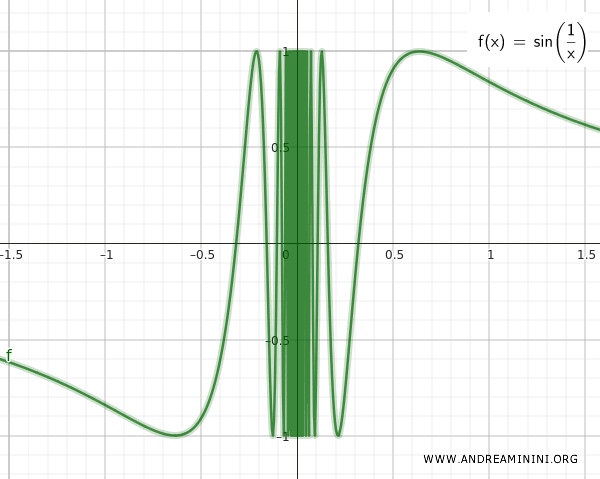
이제 두 집합의 합집합을 만들어 보자.

$$ S = Q \cup T $$

이 집합 S는 연결된 공간이다. 그 이유는, 0을 중심으로 하는 어떤 작은 구간 (0-ε, 0+ε)에도 항상 Q의 점들이 존재하기 때문이다. 즉, 0은 함수 sin(1/x)의 집적점(accumulation point)이다.

그런데도 S는 경로 연결 공간이 아니다. Q의 어느 점에서든 0으로 향하는 연속적인 경로를 정의할 수 없기 때문이다. 진동이 점점 조밀해지면서, 연속적인 경로가 끊임없이 흔들리며 0에 “닿을 수는 있어도 연결될 수는 없는” 상태가 된다.

참고: 만약 함수가 f(x)=1/x였다면 상황은 완전히 다르다. 이 경우 Q와 T는 서로 분리(disjoint)되어 있으며, 서로 가까워지지 않는다.

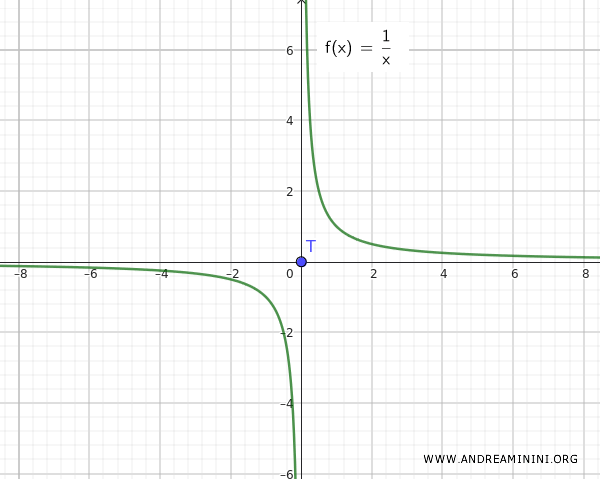
이 예시는 연결된 집합 Q={∀ x ∈ R-{0}, 1/x}와 고립된 점 T={0}의 합집합이 반드시 연결된 공간을 이루는 것은 아니라는 점을 보여 준다. 단, 그 고립된 점(예: 0)이 집적점인 경우는 예외이다.

이처럼 ‘연결’과 ‘경로 연결’은 겉보기에는 비슷하지만, 수학적으로는 전혀 다른 개념이다. 이런 미묘한 차이를 이해하는 것은 위상수학을 공부할 때 매우 중요한 출발점이 된다.