정칙 공간 (위상공간의 정칙성)

정칙성은 위상공간의 분리 능력을 설명하는 핵심 개념으로, 하우스도르프 조건보다 한층 더 세밀한 수준의 분리를 다룬다. 이러한 성질은 공간의 구조를 정교하게 이해하는 데 중요한 기준이 된다.

특히 정칙성이 있고 가산 기저를 가진 공간은 우리스온(Urysohn) 정리에 따라 계량화 가능해진다. 즉, 적절한 거리 함수를 부여할 수 있는 공간이라는 의미다.

하우스도르프 공간과의 차이

하우스도르프 조건에서는 단지 서로 다른 두 점이 서로소 열린근방을 가지면 충분하지만, 정칙성에서는 한 점과 닫힌집합까지 분리할 수 있어야 한다. 조건이 더 엄격한 만큼, 공간의 분리구조에 대한 정보를 더 깊이 제공한다.

Note. 정칙 공간은 정규 공간(normal space)과는 다르다. 정규 공간에서는 두 닫힌집합이 서로소 열린집합으로 분리될 수 있어야 하며, 이는 정칙성보다 더 강한 조건이다. 따라서 모든 정규 공간은 정칙적이지만, 모든 정칙 공간이 정규적인 것은 아니다.  

또한 정칙성과 하우스도르프 조건은 서로 독립적이다. 어떤 공간은 정칙이지만 하우스도르프가 아닐 수 있고, 반대로 하우스도르프지만 정칙성을 가지지 못할 수도 있다.

실제 예시로 살펴보는 정칙성

정칙 공간의 가장 대표적인 예는 표준위상을 지닌 실수직선 \( \mathbb{R} \)이다. 실수직선에서 정칙성이 어떻게 드러나는지 구체적으로 살펴보자.

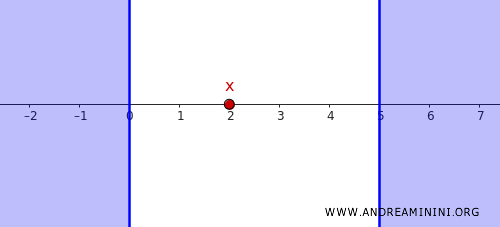
점 \( x = 2 \)와, 다음과 같은 닫힌집합 \( C \)를 생각하자.

\[ C = (-\infty, 0] \cup [5, \infty) \]

\( x = 2 \)는 분명히 \( C \)에 속하지 않으며, \( C \)는 표준위상에서 닫힌집합이다.

\( C \)의 여집합은 열린집합이므로, 우리는 쉽게 \( x \)가 포함된 열린구간을 찾을 수 있다. 예를 들어 다음 구간을 선택할 수 있다.

\[ (0,5) \]

이제 \( x = 2 \)를 가운데 두는 두 수 \( c \), \( d \)를 잡아보자.

\[ 0 < c < 2 < d < 5 \]

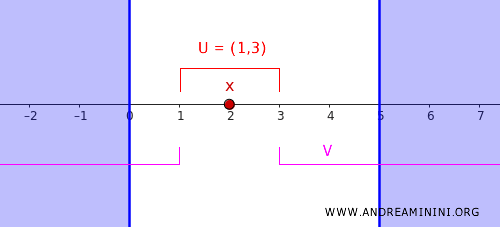
구체적으로 \( c = 1 \), \( d = 3 \)을 선택할 수 있다.

이에 따라 다음 두 열린집합을 정의한다.

• \( U = (1,3) \) : 점 \( x = 2 \)를 포함한다.
• \( V = (-\infty, 1) \cup (3, \infty) \) : \( C \) 전체가 포함된다.

이 두 집합은 서로 완전히 분리되어 있으며, 이는 실수직선이 정칙성을 만족함을 명확하게 보여준다.

Notes

정칙성을 보다 깊게 이해하기 위한 몇 가지 생각거리

• 분리공리 체계에서의 위치
  위상공간의 분리공리는 공간이 열린근방을 통해 점과 집합을 얼마나 정밀하게 구분할 수 있는지를 설명한다. 정칙성(\( T_3 \))과 하우스도르프성(\( T_2 \))은 이 체계 안에서 중요한 역할을 하며, 공간의 구조적 특성을 이해하는 데 핵심적인 기준이다.

  Note. 하우스도르프 공간에서는 서로 다른 두 점이 서로소 열린근방을 갖고, 정칙 공간에서는 점과 닫힌집합이 분리된다. 이러한 특성은 공간이 제공하는 구분 능력, 즉 공간의 '분해능'을 보여주는 중요한 지표다.

And so on.