하우스도르프 공간

하우스도르프 공간(Hausdorff space)은 서로 다른 두 점을 분리하여 각각 서로 겹치지 않는 열린 이웃을 부여할 수 있는 위상 공간이다. 이 성질은 점들이 서로 명확하게 구별되는 구조를 보장하며 위상수학에서 가장 기본적이면서도 중요한 개념 중 하나다.

핵심은 단순하다. 두 점 \( x \)와 \( y \)가 주어졌을 때, 이 두 점을 완전히 떨어뜨리는 열린 집합 \( U \)와 \( V \)를 찾을 수 있다는 것이다. 즉 \( U \cap V = \emptyset \)이 성립한다.

이 조건은 유클리드 공간에서 자연스럽게 느끼는 거리와 분리의 개념을 보다 일반적인 위상 공간에서도 그대로 사용할 수 있게 해준다.

하우스도르프 공간은 수열의 수렴이나 극한을 다룰 때 특히 유용하며, 해석학과 위상수학의 여러 정리들이 이 조건을 전제로 한다.

또 하나 중요한 사실은, 하우스도르프 공간에서는 모든 단일 원소 집합(singleton)이 닫힌 집합이라는 점이다. 어떤 점을 제외한 나머지 전체 집합이 열린 집합이 되기 때문이다.

예시

예시 1

실수선 \(\mathbb{R}\)에 정의된 표준 위상을 보자. 실수선은 우리가 가장 익숙하게 접하는 대표적인 하우스도르프 공간이다.

표준 위상에서는 단일 점이 열린 집합이 아니다. 열린 집합이 되기 위해서는 그 안의 모든 점 주변에 일정한 폭의 열린 구간이 포함되어야 하기 때문이다.

설명: 단일 점 \( \{x\} \)은 주변에 있는 어떤 점도 포함하지 않는다. 실수선에서는 두 점 사이에 항상 무수히 많은 값이 존재하므로 단일 점으로는 열린 집합을 만들 수 없다.

그러나 단일 점을 제외한 여집합 \( \mathbb{R} \setminus \{x\} \)은 열린 집합이며, 이로 인해 단일 점 \( \{x\} \)은 닫힌 집합이 된다.

또한 실수선은 하우스도르프 조건을 만족한다. 서로 다른 두 점 \( a \)와 \( b \)를 충분히 작은 열린 구간으로 둘러싸면, 두 구간을 서로 겹치지 않게 선택하는 것이 가능하다.

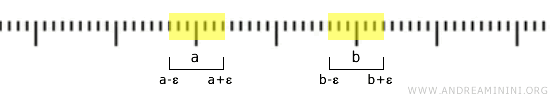
예를 들어 \( a < b \)라면 작은 \( \epsilon \)을 선택해 \( (a-\epsilon, a+\epsilon) \)과 \( (b-\epsilon, b+\epsilon) \)을 잡을 수 있고, 이때 \( a+\epsilon < b-\epsilon \)이 되도록 조절하면 두 구간은 완전히 분리된다.

따라서 표준 위상에서 단일 점이 닫힌 집합이라는 사실은 하우스도르프 공간의 성질과 정확히 들어맞는다.

예시 2

이번에는 집합 \( X = \{1,2,3\} \)에 이산 위상을 부여한 경우를 보자. 이산 위상은 구조가 매우 단순해 기본 개념을 이해하는 데 도움이 된다.

이산 위상에서는 X의 모든 부분집합이 열린 집합이다. 즉, 원소 하나짜리 집합도 열린 집합이고, 두 개짜리 집합도 열린 집합이며, 전체 집합과 공집합 역시 열린 집합이다.

• 공집합 \( \emptyset \)
• 단일 원소 집합 \( \{1\}, \{2\}, \{3\} \)
• 두 원소 집합 \( \{1,2\}, \{1,3\}, \{2,3\} \)
• 전체 집합 \( \{1,2,3\} \)

따라서 \( 2^3 = 8 \)개의 모든 부분집합이 열린 집합이 된다.

이산 위상에서는 두 점 \( x \)와 \( y \)를 각각 단일 집합 \(\{x\}\), \(\{y\}\)로 둘러싸면 되고, 이 둘은 절대 겹치지 않으므로 하우스도르프 조건이 자동으로 성립한다.

예를 들어

$$ \{1\} \cap \{2\} = \emptyset $$

이 된다.

이처럼 표준 위상에서는 모든 부분집합이 열린 집합이 되지 않지만, 이산 위상에서는 모든 부분집합이 열린 집합이 된다. 이 차이는 위상 구조의 복잡성과 성질을 이해하는 데 중요한 기준이 된다.

비고

하우스도르프 공간에서 특히 중요한 사실은, 수렴하는 수열의 극한이 항상 유일하다는 점이다. 두 개 이상의 극한을 갖는다면 서로 다른 두 점 주변에 겹치지 않는 열린 이웃을 둘 수 없기 때문이다.

증명 개요. 하우스도르프 공간 X에서 수열이 x와 y라는 서로 다른 두 점으로 수렴한다고 가정해 보자. 충분히 큰 지수 n 이후의 항들은 모두 x의 열린 이웃 A 안에도, y의 열린 이웃 B 안에도 포함되어야 한다. 그렇다면 A와 B는 서로 겹칠 수밖에 없고, 이는 하우스도르프 조건 \( A \cap B = \emptyset \)에 위배된다. 따라서 수열의 극한은 반드시 하나뿐이다.

이 성질은 위상수학 전반에서 기본 전제로 널리 활용되는 강력한 도구다.