集合の内部
位相空間 \( X \) において,集合 \( A \) の内部とは,\( A \) に含まれるすべての開集合の和集合として定義される集合である。通常,\( \text{Int}(A) \) または \( A^\circ \) と表される。
直感的に言えば,集合の内部とは,集合 \( A \) の中に完全に収まり,かつ可能な限り大きい開集合のことを指す。
\( A \) に含まれる開集合のうち,内部よりも大きなものは存在しない。
注:内部が常に開集合になるのは,その定義が「開集合の和集合」で与えられているためである。
より厳密には,集合 \( A \) の内部とは,各点の周りに \( A \) に完全に含まれる開近傍が存在するような,\( A \) のすべての点を集めた集合である。
$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ は } X \text{ において開集合である} \} $$
つまり,点 \( x \) が \( A \) の内部に属するためには,\( x \) を含み,かつ \( A \) に完全に含まれる開集合 \( U \) が少なくとも一つ存在すればよい。
ここで強調しておきたいのは,集合 \( A \) の内部は,集合そのものの性質ではなく,それを含む位相空間 \( X \) の位相構造によって決まるという点である。同じ集合 \( A \) であっても,位相が変われば内部は異なる結果になる。
具体例
\( \mathbb{R} \) に標準位相を入れた位相空間を考え,集合 \( A = [0, 1] \) を取り上げる。
この集合は,0 から 1 までのすべての実数を含む閉区間である。
この場合,集合 \( A \) の内部は開区間 \( (0, 1) \) となる。
$$ \text{Int}(A) = (0,1) $$
端点である 0 と 1 は,\( A \) に完全に含まれる開区間に含めることができないため,内部には含まれない。
例 2
次に,同じ標準位相のもとで,集合 \( A = [0, 1) \) を考える。
この集合は,0 を含み 1 を含まない左閉右開区間である。
この場合も,集合 \( A \) の内部は前の例と同じく \( (0,1) \) になる。
\[ \text{Int}(A) = (0,1) \]
内部の定義では,元の集合に完全に含まれる開集合のみを考えるため,端点 0 はここでも内部から除かれる。
注:標準位相を備えた \( \mathbb{R} \) では,開区間が基本的な開集合である。そのため,\( [0,1) \) に含まれる最大の開集合は \( (0,1) \) しか存在しない。
例 3
今度は,集合 \( A = [0,1) \) を,離散位相を備えた位相空間 \( X \) 上で考えてみる。
離散位相では,空間 \( X \) のすべての部分集合が開集合として扱われる。
その結果,集合 \( A \) の任意の点は,必ず \( A \) に完全に含まれる開近傍を持つ。
たとえば離散位相を \( \mathbb{R} \) に入れると,開区間や閉区間の区別はなくなり,空集合や点の集まり,さらには \( [0,1) \) 自身もすべて開集合となる。
したがって,この位相では集合 \( A = [0,1) \) そのものが開集合である。
この場合,集合 \( A \) の内部は \( A \) 自身に一致する。
$$ \text{Int}(A) = A = [0,1) $$
一般に,離散位相空間では,どの集合を取ってもその内部は常にその集合自身となる。
注:この例から分かるように,内部の性質は集合そのものよりも,どの位相を採用するかに強く依存している。
例 4
最後に,点集合 \( \{a, b, c\} \) からなる位相空間 \( X \) に,離散位相を入れた場合を考える。
この場合も,\( X \) のすべての部分集合が開集合となる。
- \( \emptyset \) と \( \{a, b, c\} \) は定義により開集合である。
- 各点 \( \{a\} \),\( \{b\} \),\( \{c\} \) もすべて開集合である。
- \( \{a, b\} \),\( \{a, c\} \),\( \{b, c\} \) のような部分集合も開集合となる。
この空間で集合 \( A = \{b, c\} \) を取ると,内部は次のように計算できる。
\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]
したがって,この場合も \( \text{Int}(A) = A \) が成り立つ。
注:離散位相空間では,任意の部分集合 \( S \subseteq X \) が開集合であるため,常に \( \text{Int}(S) = S \) となる。
集合の内部に関する定理
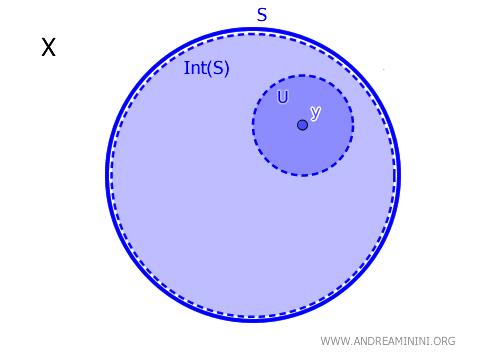
位相空間 \( X \) において,部分集合 \( S \subseteq X \) と点 \( y \in X \) を考える。点 \( y \) が \( S \) の内部 \( \text{Int}(S) \) に属するとは,\( y \in U \subseteq S \) を満たす開集合 \( U \) が存在することと同値である。すなわち,次が成り立つ。$$ y \in \text{Int}(S) \iff \exists \ U \text{ が } X \text{ における開集合であり } y \in U \subseteq S $$
要するに,点 \( y \) が集合 \( S \) の内部にあるとは,\( y \) を含む「小さな開集合」を取っても,それがすべて \( S \) の中に収まる,という状況を意味している。
この定理は,点が集合の内部に属するかどうかを判定するための,最も基本的で分かりやすい基準を与える。
証明
- 必要条件:\( y \in \text{Int}(S) \) と仮定する。内部は,\( S \) に含まれるすべての開集合の和集合として定義されている。したがって,その中には \( y \) を含む開集合 \( U \) が存在し,しかも \( U \subseteq S \) が成り立つ。
- 十分条件:\( y \in U \subseteq S \) を満たす開集合 \( U \) が存在すると仮定する。このとき \( U \) は \( S \) に含まれる開集合の一つであるから,その和集合である \( \text{Int}(S) \) にも含まれる。特に \( y \in U \) であるため,\( y \in \text{Int}(S) \) が従う。
注:この定理は,「開集合に含まれる」という局所的な視点と,「集合の内部に属する」という大域的な概念を直接結び付ける点で重要であり,連続性などの位相的概念を理解する基礎となる。
例
標準位相を備えた実数直線 \( \mathbb{R} \) において,集合 \( A = [1, 3] \) を考える。
$$ A = [1,3] $$
この集合は,1 から 3 までのすべての実数を含む閉区間である。
定理を使って,この集合の内部を具体的に求めてみよう。
そのためには,\( A \) に完全に含まれる開集合を考えればよい。
- 開集合 \( U \) の選択
\( U = (1, 3) \) を取る。これは端点を含まない開区間であり,標準位相のもとで開集合である。 - \( U \subseteq A \) の確認
任意の点 \( x \in (1, 3) \) は \( 1 < x < 3 \) を満たすため,確かに \( x \in [1, 3] \) である。
以上より,\( U \) は \( A \) に含まれる開集合である。したがって,この場合の集合 \( A \) の内部は \( (1, 3) \) となる。
注:端点 1 と 3 は,それらを含む開区間が \( A \) に完全には含まれないため,内部には含まれない。
内部に関する基本的性質
集合の内部は,ほかの基本的な位相操作と密接に関係している。ここでは,特に重要な性質をいくつか紹介する。
- 内部と和集合の関係
二つの集合 \( A, B \) に対して,それぞれの内部の和集合は,和集合 \( A \cup B \) の内部に必ず含まれる。ただし,一般には両者が等しくなるとは限らない。$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ - 内部と共通部分の関係
二つの集合の内部の共通部分は,それらの共通部分の内部と一致する。$$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$ - 補集合,内部,閉包の関係
集合 \( A \) の補集合の内部は,\( A \) の閉包の補集合に等しい。$$ \text{Int}(X - A) = X - \text{Cl}(A) $$ - 補集合の閉包と内部の補集合
集合 \( A \) の補集合の閉包は,\( A \) の内部の補集合に等しい。$$ \text{Cl}(X - A) = X - \text{Int}(A) $$
補足事項
最後に,集合の内部について理解を深めるうえで役立つ補足的な事実をまとめておく。
- 開集合は内部に含まれる
位相空間 \( X \) において,開集合 \( U \) が \( U \subseteq A \) を満たすならば,必ず \( U \subseteq \text{Int}(A) \) が成り立つ。内部は,集合 \( A \) に含まれる最大の開集合である。 - 包含関係の保存
\( A \subseteq B \) が成り立つとき,\( \text{Int}(A) \subseteq \text{Int}(B) \) が成り立つ。内部を取る操作は,集合の包含関係を保つ。 - 開集合の特徴付け
集合 \( A \) が開集合であることと,\( A = \text{Int}(A) \) が成り立つことは同値である。 - R 言語による集合の内部の計算
R 言語を用いれば,集合の内部を計算的に扱ったり,可視化したりすることも可能である。
このように,集合の内部は位相幾何学のさまざまな場面で繰り返し登場する,基本かつ重要な概念である。