開球

位相空間論で重要な概念となる開球は、中心点 c と半径 r を用いて定義される集合である。中心からの距離が r 未満である点をすべて集めたもので、円近傍や開円板と呼ばれることもある。次の式で表される。$$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

ここで扱うのは距離空間 \( M \) であり、距離関数 \( d \) は空間内の二点間の距離を測る役割を持つ。開球は中心と半径が決まれば一意に定まる、ごく基本的で扱いやすい構造である。

位相の文脈で「開いている」とは、開球の内部には、必ずそれより小さく、完全に含まれる別の開球が存在するという性質を示す。これは位相空間を理解する上で重要な直感を与えてくれる。

補足: 開球は拡大縮小や平行移動によって形状が変わっても、位相的性質そのものは変わらない。位置や大きさを調整しても開集合としての本質は保たれる。

具体的な例として、二次元空間 R² を考えてみる。点 p=(x,y) と中心 c=(x₀,y₀) の距離は、次のユークリッド距離で計算される。

$$ d(p,c) = \sqrt{(x-x_0)^2 + (y-y_0)^2} $$

開円近傍は、平面に標準的な位相構造を与える際の基本素材であり、開集合の基底として機能する。

R² の標準位相は、開球全体を基底とする位相で、平面上の最も一般的な位相として広く使われている。

$$ B = \{ B(p, r) \mid p \in R^2, \ r > 0 \} $$

ここで p は平面上の任意の点、r はその点を中心とする開球の半径である。

もちろん R² には他の位相を与えることも可能だが、この標準位相が最も広く受け入れられている理由のひとつは、開球という直感的で扱いやすい構造に基づいている点にある。

さらに、開球 B(p,r) の任意の点 $ q \in B(p,r) $ に対して、その内部に完全に収まる開球 B(q,ε) を必ず取ることができる。これは開集合の特徴をよく表している重要な性質である。

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ such \ that \ B(q,\epsilon) \subset B(p,r) $$

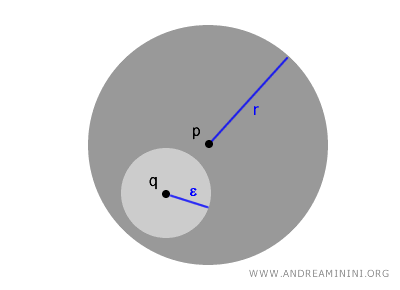
このように、開球は位相空間を理解するための出発点として極めて有用であり、その入れ子構造は開集合の直感をつかむ助けとなる。