離散位相とは何か

離散位相 T とは、集合 X に定義できる中で最も「大きな」位相であり、X のすべての部分集合をそのまま含むものです。

離散位相では、開集合の集まり T が X のあらゆる部分集合から構成されます。つまり、X のどんな部分集合も開集合として扱われます。

そのため、X の各要素はそれ自体で開集合となり、すべての点は互いに完全に独立した存在、いわば「孤立点」となります。

要素同士の距離や近さには制約がなく、どのような配置も認められます。これが「離散」という名前の由来です。

注記．集合 X 上の位相とは、X の部分集合（開集合）の集まりで、次の三つの条件を満たすものです。

離散位相は、集合上に定義できる最大の位相です。これより多くの開集合をもつ位相は存在しません。なぜなら、すでに X のすべての部分集合を含んでいるからです。

注記．これらの条件によって、開集合の体系的な構造が定まり、空間内での「近さ」や「連続性」を数学的に議論する枠組みが得られます。

離散位相の特徴

離散位相の最大の特徴は、すべての部分集合が開集合であり、同時に閉集合でもあるという点です。

離散位相では空間のすべての部分集合を開集合とみなすため、各部分集合の補集合もまた開集合になります。

位相空間では、集合の補集合が開であるとき、その集合を閉集合と呼びます。

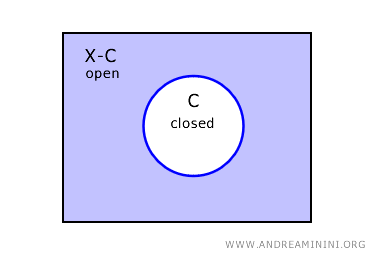
閉集合の補集合

したがって、補集合が開である以上、すべての部分集合は閉集合でもあることになります。

この性質により、離散位相の部分集合はすべて「clopen」、つまり開集合であり同時に閉集合でもあるという、非常に単純かつ明快な構造をもっています。

注記．この性質は個々の点だけでなく、任意の部分集合にも当てはまります。各点が開集合であり、点のどんな組み合わせも開集合です。また、その補集合も開集合となるため、結果としてすべての部分集合が閉集合にもなります。

ここで、3つの要素をもつ有限集合 X を考えてみましょう。

$$ X = \{a, b, c\} $$

X の冪集合、すなわち X のすべての部分集合の集合は次のようになります。

離散位相では、これらすべての部分集合が開集合です。したがって、この場合の位相 $T$ は次のように表されます。

$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \} $$

この位相では、定義上 X のすべての部分集合が開集合です。

注記．この集合族は位相の定義を満たしています。全体集合 X と空集合を含み、開集合の交わりや和集合を取っても常に T に属します。離散位相ではすべての部分集合が開集合であるため、要素間の連続性や近さに関する制約は一切存在しません。

例えば、部分集合 $ \{ a \} $ を考えてみましょう。離散位相の定義により、これは開集合です。

同時に、この部分集合 $ \{ a \} $ は閉集合でもあります。なぜなら、その補集合 $ X/ \{a\} = \{b,c\} $ が開集合だからです。

閉集合とは、開集合の補集合である集合のことです。

したがって、離散位相において部分集合 $ \{ a \} $ は開かつ閉の集合となります。

この性質は他のすべての部分集合にもあてはまります。

このように、離散位相は「すべての集合が開かつ閉である」という極めて単純な構造をもち、位相の概念を理解するうえで最も基本的な出発点となる重要な例です。