トポロジーにおける不動点

トポロジーでいう不動点とは、関数を適用しても値が変わらない点のことです。

もう少し身近に言うと、関数 f(x) があったとき、f(p) = p を満たす点 p が不動点です。p を入力すると、結果がそのまま p として返ってくる点だと考えられます。

$$ f(p) = p $$

イメージしやすい例として、ある図形を中心点 P のまわりに回転させる場面を思い浮かべてみましょう。

回転は図形の各点の位置を変えますが、中心点 P だけは常に同じ場所にとどまります。

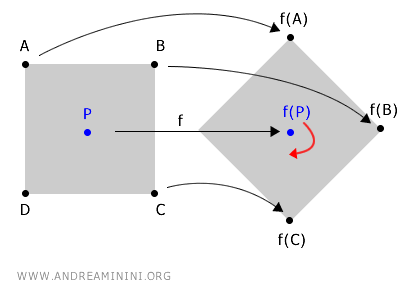
図形の回転

このように、回転写像 f によって動かない点 P は不動点として扱われます。

$$ f(P) \longrightarrow P $$

不動点という考え方は、トポロジーだけの話ではありません。数値解析、ゲーム理論、経済学など、多様な分野で基本的な役割を担っています。

トポロジーにおける代表例として有名なのが、ブラウワーの不動点定理です。

具体例

まず、閉区間 [0, 2π] を考え、関数 f(x) = sin(x) を見てみます。

$$ f(x) = \sin(x) $$

このとき p = 0 は不動点です。sin(0) = 0 となり、確かに f(p) = p が成立しています。

$$ \sin(0) = 0 $$

この例では、入力と出力がそのまま一致しています。

例 2

続いて、同じ区間 [0, 2π] で f(x) = cos(x) を考えてみます。

$$ f(x) = \cos(x) $$

こちらは x = 0 が不動点ではありません。cos(0) = 1 となり、入力と出力が一致しないためです。

しかし f(x) = cos(x) には不動点が存在し、およそ x = 0.73908513 の付近で成立します。

$$ \cos(0.73908513) = 0.73908513 $$

このように cos(0.73908513) は 0.73908513 に非常によく一致しています。

ブラウワーの不動点定理は次のように述べられます。

閉じた n 次元領域で連続な自己写像を考えると、必ず少なくとも 1 つの不動点が存在する。

この定理は「不動点が必ず存在する」という事実を保証するもので、不動点の位置までは特定しません。

それでもこの結論は重要で、動的システムや経済モデルにおける平衡状態の存在を示す際など、幅広い応用につながっています。

続きは今後さらに掘り下げていくことにします。