位相空間における同相写像(Homeomorphism)
同相写像とは、位相空間の間で定義される変換の一種であり、連続かつ全単射で、その逆写像も連続である関数を指します。
つまり、空間を「切ったり貼ったり」することなく、連続的に変形して別の空間へ写し、さらに元の空間に戻すことができる写像です。
より平易に言えば、同相写像とは、一方の空間を連続的に滑らかにもう一方の空間へ形を変えることができる対応関係であり、その過程で破損や接合は生じません。
典型的な例として、取っ手付きのコーヒーカップとドーナツ(トーラス)があります。これらは位相幾何学的に同相です。なぜなら、一方を連続的に変形することで他方に変えることができ、その逆も可能だからです。

位相的観点から見ると、両者はともに「穴」を一つ持つ図形です。ドーナツの中央の穴と、マグカップの取っ手の隙間は対応しています。取っ手部分を滑らかに変形していけば、マグカップをドーナツの形に変えることができます。
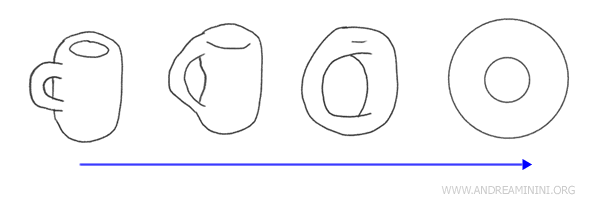
このように、二つの位相空間が同相写像によって結ばれているとき、それらは「同相な空間」と呼ばれます。つまり、見た目の形状は異なっても、位相的には本質的に同じ構造を持つということです。
同相写像の特徴
同相写像には次のような主要な性質があります。
- 全単射であること
二つの空間の要素が一対一に対応しており、一方の空間の各点が他方の空間のちょうど一つの点に対応します。 - 連続性
同相写像は連続関数であり、入力がわずかに変化すれば出力もわずかに変化します。 - 逆写像の連続性
同相写像の逆写像も連続である必要があります。これにより、変換を滑らかに逆方向へ行うことが可能になります。 - 位相的性質の保存
同相写像は、連続性、連結性、コンパクト性などの位相的性質を保ちます。したがって、元の空間における構造的な関係は、変換後の空間でもそのまま保持されます。
要するに、同相写像とは、二つの位相空間 \(X\) と \(Y\) の間の、連続かつ可逆で、逆写像も連続な全単射関数です。この性質によって、両空間の位相的特徴が保たれます。
簡潔に言えば、同相写像とは、空間を「ちぎらず」「貼らず」に形を変えられる対応関係であり、二つの図形や空間が完全に対応する関係を示します。
ここで、位相空間における連続性の定義を確認しておきましょう。
二つの位相空間 \(X\) と \(Y\) に対し、関数 \(f: X \to Y\) が、\(Y\) の任意の開集合 \(V\) について、その逆像 \(f^{-1}(V)\) が \(X\) の開集合であるとき、\(f\) は連続であると言います。
つまり、位相における連続関数とは、点を写す際に「開集合の構造」を保つ関数のことです。
したがって、位相的な連続性は、解析学で扱う距離に基づく連続性よりも一般的で抽象的な概念です。
補足:解析学では連続性は点と点の距離を基準に定義されますが、位相空間では距離の概念を必要とせず、開集合の構造によって定義されます。
具体的な例
開集合を用いて、同相写像と連続性の考え方を具体的に示してみましょう。
次の二つの位相空間を考えます:\(X = \{a, b, c, d\}\)、\(Y = \{1, 2\}\)。
- \(X\) の開集合は:\(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\)。
- \(Y\) の開集合は:\(\{\}, \{1\}, \{1, 2\}\)。
関数 \(f: X \rightarrow Y\) が連続であるとは、\(Y\) の任意の開集合に対して、その逆像が \(X\) の開集合であることを意味します。
ここで次のように関数 \(f: X \rightarrow Y\) を定義します:
\(f(a) = 1\)、\(f(b) = 1\)、\(f(c) = 2\)、\(f(d) = 2\)。
理解を助けるため、関数 \(f\) と両空間の開集合を図で示します。
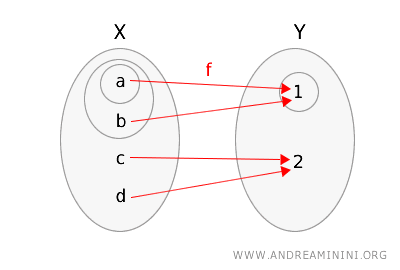
この関数が連続性の条件を満たすか確認してみましょう。
- \(Y\) の開集合 \(\{1\}\) に対する逆像は \(f^{-1}(\{1\}) = \{a, b\}\) であり、これは \(X\) において開集合です。
- \(Y\) の開集合 \(\{1, 2\}\) に対する逆像は \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\) であり、これも開集合です。
したがって、\(Y\) の任意の開集合の逆像が \(X\) の開集合であるため、この関数は連続です。
補足:空集合はすべての位相空間で開集合であるため、ここでは省略しました。
次に、別の関数 \(g: X \rightarrow Y\) を次のように定義します:
\(g(a) = 1\)、\(g(b) = 1\)、\(g(c) = 1\)、\(g(d) = 2\)。
同様に、関数 \(g\) と両空間の開集合を図で示します。
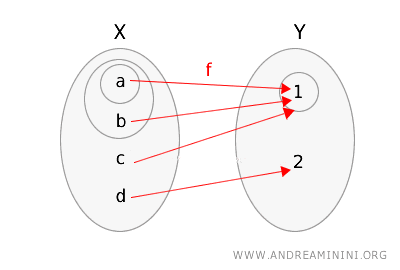
この関数が連続であるか確認してみます。
- \(Y\) の開集合 \(\{1\}\) に対する逆像は \(g^{-1}(\{1\}) = \{a, b, c\}\) ですが、これは \(X\) において開集合ではありません。
したがって、\(Y\) に少なくとも一つ、逆像が \(X\) で開集合でない開集合(この場合 \(\{1\}\))が存在するため、この関数 \(g\) は連続ではありません。
補足:まとめると、関数が連続であるとは、像の空間 \(Y\) のすべての開集合に対し、その逆像が \(X\) の開集合である場合を指します。この条件を満たさなければ連続ではありません。最初の例では \(f\) は連続でしたが、二つ目の関数 \(g\) は連続ではありませんでした。
同相写像の定義
二つの位相空間 \( X \) と \( Y \) に対し、全単射関数 \( f: X \to Y \) とその逆写像 \( f^{-1}: Y \to X \) の両方が連続であるとき、\( f \) を 同相写像 と呼び、空間 \( X \) と \( Y \) は 同相 \( X \cong Y \) であると言います。
同相な空間は位相的に同値とも呼ばれます。
では、これは何を意味するのでしょうか?
同相、すなわち位相的同値であるということは、二つの空間が位相的な観点から見て「本質的に同一の構造」を持っているということです。形や大きさが違っても、位相的には等価なのです。
この定義から、同相写像の本質的な要件が導かれます。
- 全単射であること:関数 \( f: X \to Y \) が一対一対応であり、\(X\) の各要素が \(Y\) のただ一つの要素に対応します。
- \( f \) の連続性:関数 \( f \) が連続である、すなわち \(Y\) の任意の開集合の逆像が \(X\) の開集合であること。
- \( f^{-1} \) の連続性:逆写像 \( f^{-1}: Y \to X \) も連続であること。つまり、\(X\) の任意の開集合の逆像が \(Y\) の開集合となることです。
例:紙を丸めて円筒を作る場合を考えましょう。円筒と平面の紙は同相です。なぜなら、紙を破ったり貼り合わせたりすることなく、滑らかに広げたり巻いたりして互いに変形できるからです。位相(開集合の構造)は変わらず、形だけが変化します。
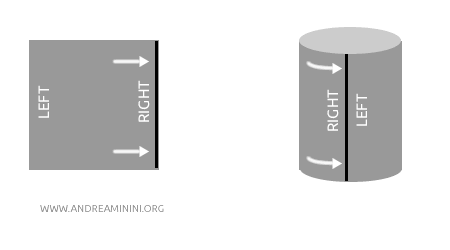
重要な注意点: 全単射 \( f \) が連続であっても、その逆写像 \( f^{-1} \) が必ずしも連続であるとは限りません。これは、\( f \) が開写像である場合に限り保証されます。
言い換えれば、関数 \( f \) が連続かつ全単射であっても、その逆写像 \( f^{-1} \) が連続であるとは限らず、したがって同相写像とは限りません。
位相空間において、関数 \( f: X \rightarrow Y \) が連続であるとは、\(Y\) のすべての開集合の逆像が \(X\) の開集合であることを意味します。
しかし、これは必ずしも \(X\) の開集合の像が \(Y\) において開集合になることを保証するものではありません。
逆写像 \( f^{-1} \) が連続であるためには、\( f \) が連続かつ全単射であるだけでなく、開写像である必要があります。
例 1
次の二つの位相空間を考えます。
- \( X = (a, b) \) に対し、位相 \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \)。
- \( Y = (1, 2) \) に対し、位相 \( T_Y = \{\emptyset, Y\} \)。
関数 \( f: X \to Y \) を \( f(a) = 1 \)、\( f(b) = 2 \) と定義します。
このとき、\( f \) は明らかに全単射です。すなわち、\( X \) の各要素が \( Y \) のただ一つの要素に対応し、逆も同様に一対一に対応します。
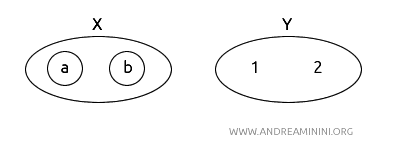
補足:図中では、開集合を円で表しています。例えば、\( X \) では {a, b}、{a}、{b} が開集合であり、\( Y \) では {1, 2} が開集合です。空集合はどの位相空間でも開集合と定義されるため、図では省略しています。
次に、関数 \( f \) およびその逆写像 \( f^{-1} \) の連続性を検討します。
- 関数 \( f \) の連続性
\( f \) が連続であるかどうかは、\( Y \) の各開集合に対する逆像が \( X \) において開集合であるかを調べることで判断できます。\( Y \) の開集合は \( \emptyset \) と \( Y \) のみです。- \( f^{-1}(\emptyset) = \emptyset \):\( T_X \) において開集合
- \( f^{-1}(Y) = X \):\( T_X \) において開集合
- 逆写像 \( f^{-1} \) の連続性
次に、逆写像 \( f^{-1}: Y \to X \) を \( f^{-1}(1) = a \)、\( f^{-1}(2) = b \) と定義します。
\( f^{-1} \) が連続であるためには、\( X \) の各開集合の逆像が \( Y \) において開集合でなければなりません。\( X \) の開集合は \( \emptyset \)、\(\{a\}\)、\(\{b\}\)、\( X \) です。- \( f^{-1}(\emptyset) = \emptyset \):\( T_Y \) において開集合
- \( f^{-1}(\{a\}) = \{1\} \):\( T_Y \) において開集合ではない(\( Y \) の開集合は \( \emptyset \) と \( Y \) のみ)
- \( f^{-1}(\{b\}) = \{2\} \):同様に開集合ではない
- \( f^{-1}(X) = Y \):\( T_Y \) において開集合
結論として、\( f \) は全単射かつ連続ですが、その逆写像 \( f^{-1} \) は連続ではないため、\( f \) は同相写像ではありません。
この例から、全単射で連続な関数であっても、逆写像が連続であるとは限らないことが分かります。
補足:この例における \( f^{-1} \) の非連続性は、\( X \) と \( Y \) の開集合の性質の違いによるものです。\( X \) には「より細かい」位相(小さい開集合)が存在しますが、\( Y \) は \( \emptyset \) と \( Y \) のみという「粗い」位相を持っています。
例 2
次に、位相の異なる別の二つの空間を考えます。
- \( X = (a, b) \) に対し、位相 \( T_X = \{\emptyset, \{a\}, X\} \)。
- \( Y = (1, 2) \) に対し、位相 \( T_Y = \{\emptyset, \{1\}, Y\} \)。
関数 \( f: X \to Y \) を \( f(a) = 1 \)、\( f(b) = 2 \) と定義します。
この関数 \( f \) も全単射です。すなわち、\( X \) の各要素が \( Y \) の一意な要素に対応します。
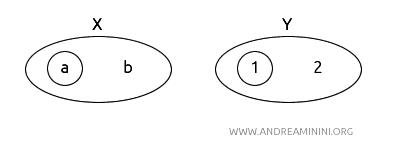
次に、\( f \) およびその逆写像 \( f^{-1} \) の連続性を確認します。
- 関数 \( f \) の連続性
\( f \) が連続であるかどうかを確認するために、\( Y \) の各開集合の逆像が \( X \) において開集合であるかを調べます。\( Y \) の開集合は \( \emptyset \)、\(\{1\}\)、\( Y \) です。- \( f^{-1}(\emptyset) = \emptyset \):\( T_X \) において開集合
- \( f^{-1}(\{1\}) = \{a\} \):\( T_X \) において開集合
- \( f^{-1}(Y) = X \):\( T_X \) において開集合
- 逆写像 \( f^{-1} \) の連続性
逆写像 \( f^{-1}: Y \to X \) を \( f^{-1}(1) = a \)、\( f^{-1}(2) = b \) と定義します。
\( f^{-1} \) が連続であるためには、\( X \) の各開集合の逆像が \( Y \) において開集合である必要があります。\( X \) の開集合は \( \emptyset \)、\(\{a\}\)、\( X \) です。- \( f^{-1}(\emptyset) = \emptyset \):\( T_Y \) において開集合
- \( f^{-1}(\{a\}) = \{1\} \):\( T_Y \) において開集合
- \( f^{-1}(X) = Y \):\( T_Y \) において開集合
したがって、この場合、\( f \) は全単射かつ連続であり、その逆写像 \( f^{-1} \) も連続です。ゆえに、\( f \) は同相写像です。
この結果が前の例と異なるのは、\( X \) と \( Y \) に与えた位相の構造が異なるためです。
補足:この例は、適切に位相を定めれば、全単射かつ連続な関数に連続な逆写像をもたせることができることを示しています。前の例では、この条件が満たされませんでした。
同相写像と他の位相変換の違い
「同相写像(homeomorphism)」という語はしばしば位相変換全般を指して用いられますが、実際にはその中の特定の種類を意味します。
位相変換と同相写像は密接に関連していますが、定義上は区別されます。
- 位相変換
位相変換はより広い概念であり、空間の連続性や連結性などの基本的性質を保ちながら、形を変化させるすべての変換を含みます。例として、同相写像のほかに、アイソトピー(isotopy)、ホモトピー(homotopy)、微分同相写像(diffeomorphism)などがあります。 - 同相写像
同相写像は、その中でも特に全単射かつ連続で、逆写像も連続な変換を指します。このような写像では、空間を切ったり貼ったりせずに可逆的な変形が可能です。したがって、同相関係にある空間は見た目が異なっていても、位相的には等価と見なされます。
すべての同相写像は位相変換の一種ですが、すべての位相変換が同相写像であるとは限りません。
一部の位相変換は、同相写像が満たす厳密な条件を欠く場合があります。
補足事項
以下に、同相写像に関連するいくつかの補足的な観点を挙げます。
- 位相的不変性(Topological property)
位相的不変性とは、同相写像によっても変化しない位相空間の性質を指します。すなわち、二つの位相空間が同相である場合(連続かつ全単射で逆写像も連続)、それらは同じ位相的性質を共有します。 - ハウスドルフの定理(Hausdorff’s Theorem)
定理によれば、もし \( f: X \to Y \) が同相写像であり、\( X \) がハウスドルフ空間であるならば、\( Y \) もまたハウスドルフ空間となります。つまり、同相写像は位相的性質を保つため、ハウスドルフ性も \( X \) から \( Y \) に伝わります。 - 抽象代数学における対応する概念は群同型(group isomorphism)です。群同型では、写像が群の演算構造を保つのに対し、同相写像では位相空間の開集合の構造を保ちます。
以上。