開集合 (Open Sets)
集合 A が 開集合であるとは、任意の要素 x が A に含まれるとき (x∈A)、x の近傍の中に A に完全に含まれるものが必ず存在することを意味します。
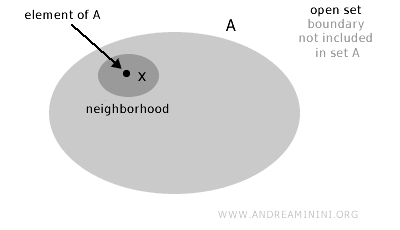
直観的には、境界点を含まない集合が開集合と呼ばれます。
より厳密には、位相空間 X における集合 A が開集合であるとは、A の任意の点 x に対し、x を含む近傍が常に A の内部に収まる場合を指します。
補足. つまり、集合内のどの点についても、外側に触れない小さな「領域」を必ず取ることができるという性質です。
具体例
一次元の場合、開集合の代表例は開区間です。
開区間とは? 実数直線 \( \mathbb{R} \) において、実数 \( a \) と \( b \) が \( a < b \) を満たすとき、\( a < x < b \) を満たすすべての実数 \( x \) からなる集合を開区間といいます。
この区間は (a,b) と表され、端点 a と b は集合に含まれません。
例えば開区間 (3,10) は実数直線上の典型的な開集合です。
この場合、集合 A は 3 と 10 の間にある無数の実数から構成されます。ただし端点は含みません。
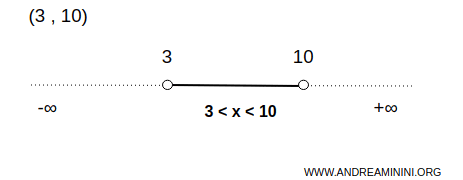
この区間に属する任意の点 x について、常に (3,10) に完全に含まれる小さな開区間を取ることができます。
例えば x=3.1 の場合、(3.09,3.11) のような区間は確かに (3,10) に収まっています。
この性質は (3,10) の任意の点に対して成り立ちます。なぜなら任意の 2 つの実数の間には常に無数の実数が存在するからです。
補足. 仮に (3,10) の中の極めて端に近い点、例えば 3.001 を考えても、3.001±0.00000001 のように無数の点を含む近傍を取ることができ、それは必ず (3,10) の内部に収まります。
これは一次元空間における開集合の最も基本的な例です。
その他の例
同じ考え方は二次元にも拡張できます。
例えば原点 (0,0) を中心とし半径 r=1 の円板を考えます。
$$ x^2+y^2<1 $$
この不等式は中心からの距離が 1 より小さい点全体を表し、円周上の点を含まず内部のみを含むため開集合となります。
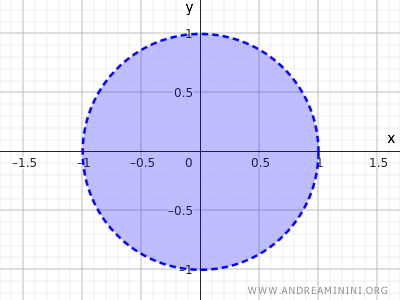
これも開集合の一例です。
閉集合とは?
閉集合を得るには、円周上の点も含めれば十分です。
$$ x^2+y^2 \le 1 $$
この場合、集合内のすべての点が近傍を持つとは限らなくなります。
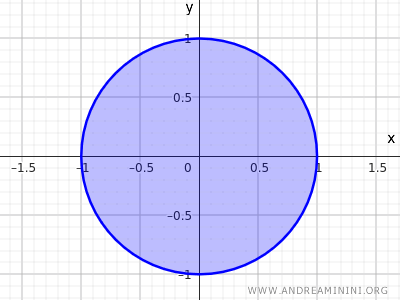
閉集合の場合、円周上の点には集合に完全に含まれる近傍が存在しません。
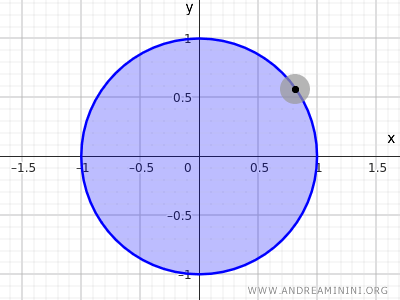
補足. 方程式 \( x^2+y^2=1 \) で表される円周上の点だけの集合は、内部を含まないため \( \mathbb{R}^2 \) の通常の位相では開集合でも閉集合でもありません。一方、不等式 \( x^2+y^2<1 \) による集合は円周を含まないため開集合の例となり、逆に \( x^2+y^2\le 1 \) の集合は円周を含むため閉集合となります。
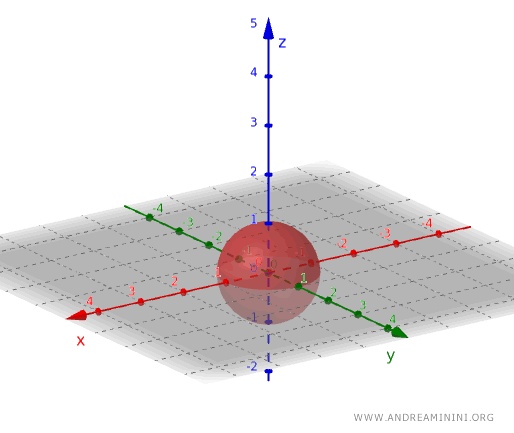
同様に三次元でも、球の内部だけを取り、表面を含めなければ開集合が得られます。
位相という視点
開区間は直観的で理解しやすいため、開集合の概念を学ぶ出発点として適しています。
しかし、開集合という概念は本来より抽象的であり、開区間や円板に限られるものではありません。
基本をつかんだら、より一般的な観点から考える必要があります。
集合が「開」であるかどうかは、その空間にどの位相を導入するかに依存します。
重要なのは、開集合の定義は採用する位相によって大きく変化しうるという点です。
位相が変われば、標準的には「閉じている」と見なされる集合が「開」として扱われる場合もあります。
言い換えると、どの集合であっても、選ばれた位相次第で開集合とみなすことが可能です。
位相とは? 位相とは、ある空間に対して「開集合」と見なす部分集合の族のことです。これらは、開集合の任意の和が開であることや、有限個の開集合の共通部分が開であることなど、いくつかの公理を満たします。
したがって、開区間や開円板といった直観的な例だけに思考を限定しないことが大切です。
位相空間では、見た目の印象とは異なり開集合として扱われる場合があるからです。
別の具体例
2 要素からなる集合 \( \{a, b\} \) を考えます。
この集合には最低でも 2 種類の位相が定義できます。自明位相と離散位相です。
- 自明位相
自明位相では、開集合は空集合 \( \emptyset \) と全体集合 \( \{a, b\} \) のみです。最も単純で、開集合の構造がほとんど存在しません。 - 離散位相
離散位相では、\( \{a, b\} \) のすべての部分集合が開集合です。つまり \( \{a\} \)、\( \{b\} \)、\( \{a, b\} \)、そして \( \emptyset \) がすべて開集合となります。最も自由度が高い位相です。
次に、集合 \( \{a\} \) を両者で比較してみます。
- 自明位相では {a} は開集合ではない
開集合として認められるのは \( \emptyset \) と \( \{a, b\} \) だけです。 - 離散位相では {a} は開集合である
離散位相では全ての部分集合が定義上開集合です。
したがって同じ集合 \( \{a\} \) であっても、自明位相では開ではなく、離散位相では開となります。
この単純な例から、開集合の概念が位相の選択と不可分であることがよく分かります。
開集合に関する定理 (Open Set Theorem)
定理 1
開集合 X とその上の位相 T により位相空間 (X, T) が定まっているとする。このとき部分集合 S⊂X が開集合であるとは、任意の点 s∈S に対して、s を含み、かつ S の内部に完全に収まる近傍 U が存在すること、すなわち U⊂S を満たすことである。
この条件を満たすとき、S は位相空間 (X, T) に属する開集合であると定義される。
したがって、部分集合 S に含まれる任意の点 s∈S は、自身の近傍を S の内部に確保できるという意味で、S をその点の近傍としてみなすことができる。
特に任意の点 s∈S に対し、その近傍 Us は S の内部に含まれる開集合である。
$$ x \in U_s \subset S \subset X $$
開集合は、このような開近傍の和集合として表すことができる。
したがって、部分集合 S の各点が S に収まる近傍 Us を持つならば、S はそれらの近傍の和集合となるため開集合であると結論できる。
換言すれば、集合が開であることと、集合内の任意の点がその点を完全に含む近傍を持つことは同値である。
例. テーブルの上にビー玉が散らばっている様子を想像してほしい。各ビー玉を集合の点と考える。集合が「開」であるとは、どのビー玉のまわりにも、テーブルの端に触れない範囲で円を描ける状態に相当する。すべてのビー玉についてこのような円を描けるなら、その集合は開集合であるといえる。つまり開集合とは、どの点を選んでも、その周囲に常に集合内部の「自由な領域」が確保されている状態である。

定理 2
集合 \( X \) と、その上の位相を定める基底 \( B \) を考える。部分集合 \( A \subset X \) が、基底 \( B \) によって生成される位相における開集合であるための必要十分条件は、任意の点 \( x \in A \) に対して、\( x \) を含み、しかも \( A \) に完全に含まれる基底要素 \( B_x \in B \) が存在すること、すなわち \( B_x \subseteq A \) を満たすことである。
この定理は、基底によって得られる位相の特徴を端的に示している。
平たく言えば、開集合 \( A \) の各点は、基底要素のひとつに含まれていなければならず、その基底要素は集合 \( A \) の内部に完全に収まっていなければならない。
この条件が成り立つとき、\( A \) は基底 \( B \) によって生成された位相における開集合であることが保証される。
証明. A が基底 B によって生成された位相における開集合であるとする。このとき定義より A は基底要素の和集合として記述される。したがって任意の点 x∈A は少なくともひとつの基底要素 Bx に含まれ、しかも Bx は A の内部に完全に収まっている。逆に、任意の点 x∈A が A に含まれる基底要素 Bx に属するなら、A はそれらの基底要素の和集合となり開集合である。よって必要十分性が示される。
例
集合 \( X = \{1, 2, 3, 4, 5\} \) に対し、基底を \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) とする。このとき \( A = \{1, 2, 3\} \) が開であるかを判定する。
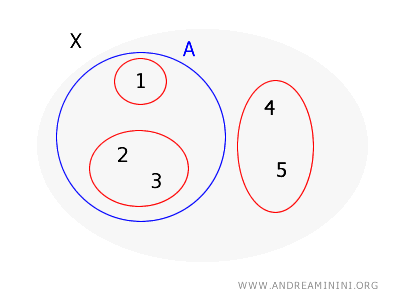
各点について次を確認する:
- 点 \( 1 \) は基底要素 \( \{1\} \) に含まれ、これは A の内部に収まる。
- 点 \( 2 \) は基底要素 \( \{2, 3\} \) に含まれ、これは A の内部に収まる。
- 点 \( 3 \) も同じ基底要素 \( \{2, 3\} \) により条件を満たす。
以上より、\( A \) は基底 \( B \) が生成する位相における開集合であるといえる。
例 2
同じ集合 \( X = \{1, 2, 3, 4, 5\} \) に対し、再び基底 \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) を考える。
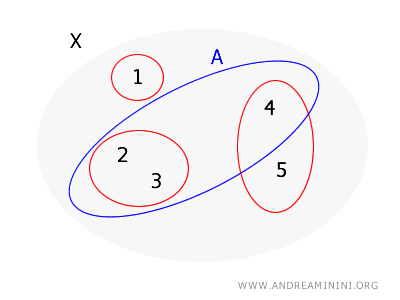
このとき \( A = \{2, 3, 4\} \) が開であるかを判定する:
- 点 \( 2 \) は基底要素 \( \{2, 3\} \) によって条件を満たす。
- 点 \( 3 \) も同じ基底要素 \( \{2, 3\} \) によって条件を満たす。
- しかし点 \( 4 \) の場合、これを含む基底要素は \( \{4, 5\} \) だけであり、これは A の内部に収まらない (要素 5 を含むため)。
よって条件を満たさない点が存在するため、\( A \) は開集合ではないと結論づけられる。
補足
開集合に関する付記:
- 集合 A が開であることと A = Int(A) は同値
位相空間 \( X \) の部分集合 \( A \) が開であるとは、A がその内部 Int(A) と一致することを意味する。内部 Int(A) とは、A に含まれるすべての開集合の和集合である。$$ A = \text{Int}(A) $$
この議論はさらに発展していく。