集合の閉包

位相空間 \( X \) における集合 \( A \) の閉包とは、\( A \) を含むすべての閉集合の共通部分として定義される集合である。通常、この集合を \( \text{Cl}(A) \) と表す。

直感的に言えば、集合 \( A \) の閉包とは、\( A \) を完全に含む閉集合のうち、最も小さいものを意味する。

すなわち、\( A \) を含む閉集合の中で、これ以上小さな閉集合は存在しない。

注: この性質は定義から直ちに理解できる。閉包は、\( A \) を含むすべての閉集合の共通部分として作られるためである。閉包は、集合 \( A \) の周囲を可能な限り最小限に包み込む閉集合と考えることができる。

形式的には、集合 \( A \) の閉包は次のように定義される。

$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ and } C \text{ is closed in } X \} $$

ここで \( \bigcap \) は共通部分を表し、\( A \) を含むすべての閉集合 \( C \) に共通して属する点全体を意味する。

閉包 \( \text{Cl}(A) \) には、集合 \( A \) 自身に加えて、位相空間 \( X \) における \( A \) のすべての極限点が含まれる。

注: 重要な点として、閉包は集合 \( A \) そのものの性質よりも、それが置かれている位相空間 \( X \) の構造に強く依存する。そのため、同じ集合 \( A \) であっても、位相が変われば閉包も異なり得る。

具体例

実数全体 \( \mathbb{R} \) に標準位相を入れた位相空間において、集合 \( A = (0, 1) \) を考える。

これは、0 と 1 を含まない実数全体からなる開区間である。

この場合、集合 \( A \) の閉包は次のようになる。

$$ \text{Cl}(A) = [0,1] $$

元の開区間 \( (0,1) \) に加えて、境界に位置する点 0 と 1 が集積点として含まれるためである。

注: 標準位相における閉集合とは、すべての極限点を含む集合である。例えば、閉区間 [0,2] と [-1,1] の共通部分は [0,1] となる。 $$ [0,2] \cap [-1,1]=[0,1] $$ 開区間 (0,1) を含むこれより小さな閉集合は存在しない。

例 2

同じく標準位相を入れた \( \mathbb{R} \) において、集合 \( A = [0,1) \) を考える。

この集合は、0 を含み 1 を含まない左閉右開区間である。

この場合も閉包は次のようになる。

$$ \text{Cl}(A) = [0,1] $$

点 0 はすでに集合に含まれているが、点 1 は集合の外部にある極限点であるため、閉包には新たに 1 が加わる。

したがって、[0,1] が \( A \) を含む最小の閉集合となる。

注: この結果は、閉包が集合のすべての集積点を含むという基本的な考え方と一致している。

例 3

次に、同じ集合 \( A = [0,1) \) を、離散位相をもつ位相空間 \( X \) の中で考える。

離散位相では、位相空間のすべての部分集合が開集合であり、同時に閉集合でもある。

• 開集合
  離散位相では、\( X \) の任意の部分集合が開集合となる。したがって、集合 \( A \) も開集合である。
• 閉集合
  同様に、任意の部分集合は閉集合でもある。補集合が常に開集合になるためである。

このように、開集合かつ閉集合である集合を clopen 集合と呼ぶ。

その結果、この場合の閉包は集合 \( A \) 自身となる。

$$ \text{Cl}(A) = [0,1) $$

集合を閉じるために新たな点を加える必要がないからである。

注: この例は、位相の選び方によって閉包が大きく変わることを分かりやすく示している。

例 4

点集合 \( \{a, b, c\} \) からなる位相空間 \( X \) に、離散位相を入れた場合を考える。

この位相では、\( X \) のすべての部分集合が開集合であり、同時に閉集合でもある。

• \( \emptyset \) と \( \{a, b, c\} \) は開集合である。
• 各一点集合 \( \{a\} \)、\( \{b\} \)、\( \{c\} \) も開集合である。
• \( \{a, b\} \)、\( \{a, c\} \)、\( \{b, c\} \) などの集合もすべて開集合である。

このため、どの集合もすでに閉集合でもある。

集合 \( A = \{b, c\} \) は開集合であり、その補集合 \( X/A = \{a\} \) も開集合であるため、\( A \) は閉集合でもある。

したがって、集合 \( A \) の閉包は新たな点を加える必要がなく、次のようになる。

\[ \text{Cl}(A) = \{b, c\} \]

この位相では、すべての集合が最初から開かつ閉であるため、閉包操作は実質的に何も変えない。

注: 実際に、\( A \) を含む閉集合は \( \{b, c\} \) と \( \{a,b,c\} \) のみであり、その共通部分は \( \{b, c\} \) となる。 $$ \text{Cl}(A) = \{b,c\} \cap \{a,b,c\} = \{b, c\} $$ よって、確かに \( \text{Cl}(A) = A \) である。

集合の閉包に関する定理

位相空間 \( X \) において、点 \( y \) が部分集合 \( S \) の閉包 \( \text{Cl}(S) \) に属するのは、かつそのときに限り、\( y \) を含む任意の開集合 \( U \) が \( S \) と空でない共通部分をもつ場合である。すなわち、 \( y \in \text{Cl}(S) \iff \forall\, U \text{（開集合）で } y \in U,\ U \cap S \neq \emptyset \) が成り立つ。

より平易に言えば、点 \( y \) が集合 \( S \) の閉包に含まれるためには、\( y \) のまわりにどのような開集合を取っても、必ずその中に \( S \) の点が現れなければならない。

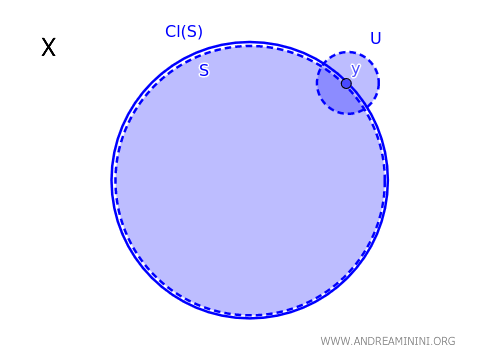
この定理は、位相空間において「ある点が閉包に属するかどうか」を調べる際の、直感的かつ強力な判定基準を与えてくれる。

証明

• 必要条件：\( y \in \text{Cl}(S) \) と仮定する。閉包の定義より、\( y \) を含む任意の開集合は必ず \( S \) と交わる。閉包は集合 \( S \) の点だけでなく、その極限点もすべて含む集合であり、極限点とは「その点を含む任意の近傍が必ず集合と交わる点」として定義される。
• 十分条件：逆に、\( y \) を含む任意の開集合が \( S \) と交わると仮定する。このとき \( y \) は \( S \) の極限点であるか、あるいは \( S \) 自身の元である。いずれの場合も、定義により \( y \) は \( \text{Cl}(S) \) に属する。

注: この定理は位相幾何学の基礎をなす重要な結果であり、開集合という局所的な概念と、閉包という大域的な構造とを直接結び付けている。連続性、収束、極限といった概念の理解に不可欠であり、多くの定理の証明で繰り返し用いられる。

例

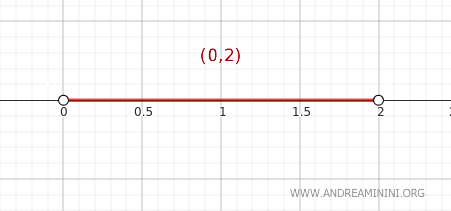
標準位相を入れた実数全体 \( \mathbb{R} \) において、集合 \( A = (0, 2) \) を考える。これは実数直線上の開区間である。

閉包の定理を用いて、点 \( y \) が集合 \( A \) の閉包 \( \text{Cl}(A) \) に属するかどうかを調べてみる。

具体的に、点 \( y = 2 \) を考える。

定理によれば、\( y \in \text{Cl}(A) \) が成り立つためには、\( y \) を含むすべての開集合 \( U \) が \( A \) と交わらなければならない。

1. 開集合の確認：\( y = 2 \) を含む開集合として、\( (1.9, 2.1) \)、\( (1.95, 2.05) \)、\( (1.99, 2.01) \) などを考える。これらはいずれも区間 \( A = (0,2) \) に属する点を含んでいる。
2. 交わりの成立：このように、どの開集合を選んでも必ず \( A \) と交わるため、定理より \( y = 2 \) は \( \text{Cl}(A) \) に属することが分かる。

したがって、点 \( y = 2 \) は集合 \( A \) の閉包に含まれる。

$$ y \in \text{Cl}(A) $$

実際、集合 \( A \) の閉包は閉区間 \( \text{Cl}(A) = [0, 2] \) であり、この中には点 \( y = 2 \) が含まれている。

位相空間における閉包の基本的性質

ここでは、閉包に関する基本的な性質と、内部や補集合といった操作との関係を整理する。これらは位相的議論を理解する上で欠かせない事項である。

• 補集合の内部と閉包の補集合
  集合 \( A \) の補集合の内部は、\( A \) の閉包の補集合に一致する。 $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$
• 補集合の閉包と内部の補集合
  集合 \( A \) の補集合の閉包は、\( A \) の内部の補集合に等しい。 $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$

重要な性質のまとめ

最後に、閉包に関する代表的な性質を簡潔にまとめておく。

• \( C \) が閉集合で \( A \subseteq C \) ならば \( \text{Cl}(A) \subseteq C \)
  閉包は集合 \( A \) を含む最小の閉集合であるため、すでに閉である集合 \( C \) を超えることはない。
• \( A \subseteq B \) ならば \( \text{Cl}(A) \subseteq \text{Cl}(B) \)
  集合の包含関係は、その閉包に対しても保存される。
• 集合 \( A \) が閉であることと \( A = \text{Cl}(A) \) は同値
  閉集合とは、そのすべての極限点を含む集合である。
• 閉包は集合と極限点の和集合
  $$ \text{Cl}(A) = A \cup A' $$
• 冪等性
  $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$
• 包含性
  $$ A \subseteq \text{Cl}(A) $$

続編あり。