位相の基底

位相の基底とは、位相空間 T において、T に含まれる任意の開集合が基底 B の要素の和集合として表されるような開集合族 B を指します。

集合 X と、その部分集合族 T によって X 上に位相を定めるとき、位相 T の基底とは、次の条件を満たす集合族 B であり、これらの集合は基底要素と呼ばれます。

• X の任意の点 x は、必ず B に属するいずれかの集合に含まれていなければならない。
• B に属する二つの集合 B₁, B₂ の非空な共通部分 B₁∩B₂ に x が属する場合、その共通部分内に x を含む別の基底要素 B₃ が存在しなければならない。
  

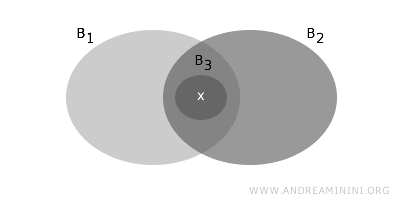
これらの条件により、B が位相 T を生成する基底として適切に機能することが保証されます。

この性質が重要な理由

基底を用いることで、位相 T に含まれるすべての開集合を直接列挙する必要はなく、基底要素の和集合として簡潔に構成できます。これは位相を扱う上で極めて有効な方法です。

注意. 基底要素の交差に関する条件は、「二つの開集合の共通部分も開集合である」という位相の基本公理を確保するために欠かせません。

具体例

集合 X を

$$ \{a, b, c \} $$

とし、位相 T を

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

のように定めます。

このとき、T は X のすべての開集合を表し、各集合は開集合として定義されています。

この位相の基底 B の一例は次のようになります。

$$ B = \{ \{ a \} ,\{ b,c \} \} $$

この基底は、X={a,b,c} の各要素が B のいずれかに含まれるという条件を満たしています。また、二つの基底要素の交差が存在しないため、第二条件も自動的に満たされます。

T に属するすべての開集合は B の要素の和集合として与えられます。

例えば:

$$ \{ a \} \in B $$

$$ \{ b,c \} \in B $$

$$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

注意. 空集合 Ø は任意の集合の真部分集合でない部分集合であり、位相の公理により必ず開集合として含まれます。したがって基底にも含めることができます。 $$ \emptyset \in B $$

この例は、有限集合上の基本的な位相構造と基底の役割を示すものです。

無限集合やより高度な位相空間では基底はさらに重要になりますが、基本的な考え方は同じであり、基底は開集合の「構成単位」として理解できます。

別の基底の構成例

集合 X={a,b,c} に対する別の基底 B を次のように取ることもできます。

$$ B = \{ \{ a \} ,\{ b \}, \{ c \} \} $$

これは単元集合のみから成る基底であり、以下の点から T={ Ø,X,{a},{b,c}} の基底であることが分かります。

• 空集合 Ø は定義により開集合であり、基底によらず常に位相に含まれる。
• {a} は B に含まれている。 $$ \{ a \} \in B $$
• {b,c} は B の {b} と {c} の和集合として表される。 $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
• X={a,b,c} も同様に {a}, {b}, {c} の和集合として表される。 $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

注意. 一つの位相に対して複数の基底が存在し得ることは重要であり、それぞれ異なる観点から開集合の生成方法を与えます。

例 2

a< b を満たす実数の開区間 (a,b) からなる集合を考えます。

$$ B=\{ (a,b) \subset R \mid a < b \} $$

任意の実数点は必ず何らかの開区間に含まれるため、この集合は実数直線の標準位相を与える基底となります。

さらに、二つの開区間が交差する場合、その交差部分に含まれる点も、それを含む別の開区間として基底 B の要素で捉えることができます。

例えば、開区間 (0,3) と (2,4) の交差は (2,3) となります。

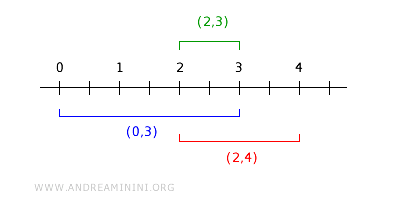
区間 (2,3) は基底要素 B_i の一つであり、明らかに交差部分に含まれます。
$$ (0,3) \cap (2,4) = (2,3) \in B_i \subset (0,3) \cap (2,4) $$

可算基底

可算基底とは、位相空間 \( X \) に対する開集合のうち、可算集合 \( \mathcal{B}=\{B_1,B_2,B_3,\dots\} \) から構成される基底を指します。任意の開集合はこれらの基底要素の和集合として表せます。

集合が「可算」であるとは、有限集合である場合か、自然数集合 \( \mathbb{N} \) と一対一対応が取れる場合を指します。

したがって、集合を \( B_1,B_2,B_3,\dots \) と番号付けできるなら、その集合族は可算です。

基底と可算基底の違い

基底は位相を生成する集合族ですが、特にその基底を構成する集合が可算個に限られるとき、可算基底と呼ばれます。

重要性. 可算基底をもつ位相空間は解析学や位相数学において扱いやすく、多くの定理がこの仮定のもとで成立します。ウリソーンの距離化定理でも可算基底は重要な条件となっています。

例

標準位相をもつ \( \mathbb{R} \) において、有理数 \( a,b\in\mathbb{Q} \) を端点とし、a< b を満たす開区間 (a,b) の集合は可算基底を与えます。

これは、これらの区間を I₁, I₂, I₃,… のように順に並べることができるためです。

証明の概要

自然数は

\[ 1,\ 2,\ 3,\ 4,\ 5,\ \dots \]

のように順序付けできるため可算です。

同様に、有理数端点をもつ開区間 (a,b) 全体が列挙できれば、この集合も可算となります。

有理数は無限ですが、例えば次のようにして列挙できます。

\[ 0,\ 1,\ -1,\ \tfrac{1}{2},\ -\tfrac{1}{2},\ \tfrac{2}{3},\ -\tfrac{2}{3},\ \dots \]

これらを \( q_1,q_2,q_3,\dots \) とおきます。

そして、すべての組 (q_i,q_j) のうちで q_i < q_j を満たすものを取り出します。

• \( (q_1,q_2)=(0,1) \)
• \( (q_3,q_2)=(-1,1) \)
• \( (q_4,q_5)=(\tfrac{1}{2},-\tfrac{1}{2}) \) ❌ 不適格（端点が逆）
• \( (q_5,q_1)=(-\tfrac{1}{2},0) \)
• ...

条件 a< b を満たす組のみを用いれば、開区間の列挙が可能です。

列挙すると次のようになります。

1. \( (0,1) \)
2. \( (-1,1) \)
3. \( (-\tfrac{1}{2},0) \)
4. \( (0,\tfrac{1}{2}) \)
5. \( (-1,\tfrac{1}{2}) \)
6. \( (\tfrac{1}{2},1) \)
7. \( (-\tfrac{2}{3},0) \)
8. \( (0,\tfrac{2}{3}) \)
9. \( (-1,\tfrac{2}{3}) \)
10. \( (-\tfrac{1}{2},\tfrac{1}{2}) \)
11. ...

このように、無限に存在する区間でも自然数と同様に順に並べられるため、可算であることが分かります。

したがって、端点が有理数で a< b を満たすすべての開区間 (a,b) からなる集合は可算基底を構成します。

補足

位相の基底に関する追加の観察を挙げます。

• 集合 X の各要素 x に対し、{x} をすべて基底 B に含めると、X 上の任意の位相 T を生成できる基底が得られます。

  単元集合の和集合によって、X 上に取り得るどの位相も生成できます。
  
  例えば、X={a,b,c} に対して B={ {a},{b},{c} } とすると、位相 T={Ø,{a},{b,c},X} を生成します。
  
  同じ基底 B は、位相 T={Ø,{b},{a,c},X}、自明位相 T={Ø,X}、離散位相 T={Ø,{a},{b},{c},{a,b},{a,c},{b,c},X} など、X 上に定義できるその他の位相も生成します。

  注意. 第一条件は、X の各点が必ず B のいずれかに含まれるため満たされます。第二条件も、単元集合同士は互いに交わらないため自動的に満たされます。

以上のように、基底の概念はさらに広範な状況にも自然に拡張できます。